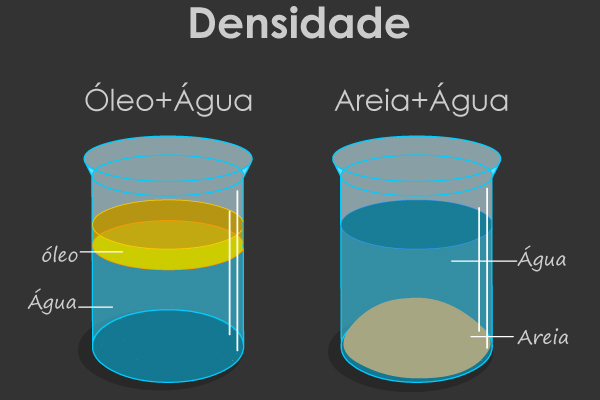
No texto Densidade, foi mostrado que essa grandeza é a relação entre a massa de um material e o volume por ele ocupado (densidade = massa/volume).
Assim, calcular a densidade de líquidos e de sólidos regulares é fácil. Os líquidos podem ser “pesados” em uma balança, descobrindo sua massa, e medidos em algum cilindro graduado, como uma pipeta ou proveta, para descobrir seu volume. Depois é só jogar na fórmula da densidade.
Já os sólidos regulares podem também ser “pesados” na balança para se descobrir sua massa, e seu volume é dado por meio de fórmulas específicas. Por exemplo, se for um cubo ou um paralelepípedo, basta medir a altura (h), o comprimento (c) e a largura (l), multiplicando essas três grandezas. Isso é mostrado logo mais abaixo, bem como as fórmulas para se calcular o volume de outros tipos de sólidos regulares:
.jpg)
Nas fórmulas acima, “b” corresponde à base (por exemplo, se a base da pirâmide for de quatro lados, então b = 4), “r” é o raio e “π” é igual a 3,14.
Mas e se o sólido for irregular, como uma pedra, por exemplo? Como descobriremos seu volume e, consequentemente, como iremos calcular sua densidade?
Nesse caso, não se desespere, pois existe uma forma bem simples de determinar o volume de sólidos irregulares, que é o Princípio de Arquimedes, chamado assim porque foi descoberto no século III a. C. por esse matemático grego. Ele descobriu que o volume de água deslocado por um sólido irregular é exatamente igual ao volume do próprio sólido.

Um selo impresso na Grécia que mostra Arquimedes de Siracusa e atrás a sua descoberta do volume de sólidos irregulares, por volta de 1983 *
Por exemplo, digamos que você quer descobrir a densidade de um pedaço de ferro de forma irregular. Depois de determinar a massa desse objeto, você determinará o volume dele fazendo o seguinte:
- Coloque determinado volume de água em uma proveta;
- Depois pegue o pedaço de ferro e coloque-o totalmente submerso nessa proveta;
- Observe qual foi a diferença no volume da água. Pronto! Esse é o volume do sólido!

Por exemplo, digamos que a massa “pesada” deu igual a 39,5 g e que o volume de água na proveta aumentou de 50 mL para 55 mL, então a diferença do volume, isto é, 5 mL, corresponde ao volume do pedaço de ferro. Calculando a densidade dele, temos:
d = m
V
d = 39,5 g
5 mL
d = 7,9 g/mL
Essa é exatamente a densidade do ferro a 20ºC.
Pode-se dizer também que quanto menos o volume de água for deslocado, menos denso é o objeto.
* Créditos da imagem: Lefteris Papaulakis / Shutterstock.com