Cálculo de partículas alfa e beta

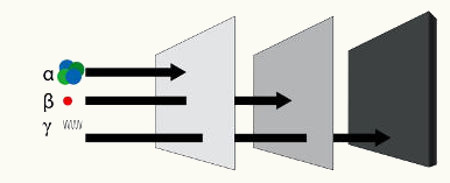
 Quando um determinado material é radioativo, a tendência é a de que ele elimine as radiações alfa, beta e gama. Essas radiações são eliminadas a partir do núcleo do átomo em decorrência da instabilidade nuclear dos átomos do material.

Conhecendo um pouco os materiais radioativos, podemos calcular, por exemplo, o número de partículas alfa e beta que serão eliminadas a partir do núcleo de um átomo. Para isso, é importante saber as composições de cada tipo de radiação:

• Radiação alfa: composta por dois prótons (número atômico 2) e dois nêutrons, resultando em número de massa 4, assim: ₂α⁴

• Radiação beta: composta por um elétron, resultando em número atômico -1 e número de massa 0, assim: _-1β⁰

Conhecendo as partículas, percebemos que: quando um átomo elimina radiação alfa (primeira lei de Soddy), forma um novo elemento cujo número atômico será duas unidades menor e o número de massa será quatro unidades menor. Ao eliminar uma radiação beta (segunda lei de Soddy), o átomo formará um novo elemento cujo número atômico terá uma unidade a mais e sua massa permanecerá a mesma.

♦ Primeira lei: _ZX^A → ₂α⁴ + _Z-2Y^A-4

♦ Segunda lei: _ZX^A → _-1β⁰ + _Z+1Y^A

Vale lembrar que a eliminação de partículas alfa e beta é simultânea e sempre um novo elemento será originado. Se esse elemento originado for radioativo, a eliminação de radiação continuará até que se forme um átomo estável.

Com todas essas informações dadas, podemos agora calcular o número de partículas alfa e beta que foram eliminadas por um material radioativo até que um átomo estável tenha sido formado.

Para isso, utilizamos a seguinte equação:

_ZX^A → c₂α⁴ + d_-1β⁰ + _bY^a

Z = Número atômico do material radioativo inicial;

A = Número de massa inicial do material radioativo inicial;

c = Número de partículas alfa eliminadas;

d = Número de partículas beta eliminadas;

a = Número de massa do elemento estável formado;

b = Número atômico do elemento estável formado.

Como a soma dos números de massa antes e depois da seta são iguais, temos que:

A = c.4 + d.0 + a

A = 4c + a

(conhecendo A e a, podemos determinar o número de partículas alfa eliminadas)

Como a soma dos números atômicos antes e depois da seta são iguais, temos que:

Z = c.2 + d.(-1) + b

Z = 2c – d + b

(conhecendo Z, c e b, podemos determinar o número de partículas beta eliminadas)

Veja um exemplo:

Determine o número de partículas alfa e beta que foram eliminadas por um átomo de rádio (₈₆Rn²²⁶) para que ele fosse transformado em um átomo ₈₄X²¹⁰.

Dados do exercício: o átomo radioativo inicial é o Rn e o formado é o X, assim:

Z = 86

A = 226

c = ?

d = ?

a = 210

b = 84

Inicialmente determinamos o número de partículas alfa:

A = 4c + a

226 = 4c + 210

4c = 226 -210

4c = 16

c = 16
      4

c = 4 (partículas alfa)

Em seguida, calculamos o número de partículas beta:

Z = 2c – d + b

86 = 2.4 – d + 84

86 – 84 – 8 = - d .(-1 para eliminar o negativo do d)

d = 6 (partículas beta)