Cálculo do número de partículas em uma solução

Realizar o cálculo do número de partículas em uma solução é importante porque a quantidade de soluto determina o comportamento físico do solvente com relação ao ponto de fusão, ao ponto de ebulição, à pressão osmótica e à pressão máxima de vapor.

O estudo sobre o cálculo do número de partículas em uma solução ocorreu juntamente com a descoberta das chamadas propriedades coligativas (tonoscopia, ebulioscopia, crioscopia e osmoscopia).

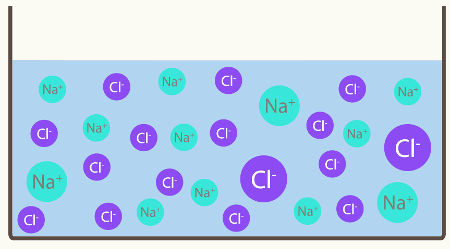
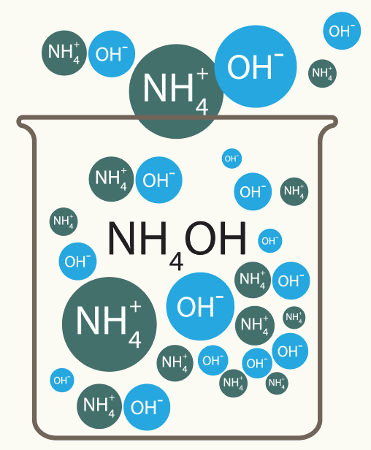
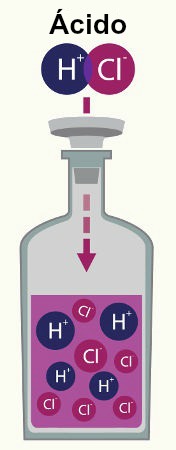
Para calcular o número de partículas em uma solução, devemos levar em consideração a natureza do soluto que foi dissolvido no solvente, ou seja, se ele é iônico ou molecular.

O conhecimento da natureza do soluto é relevante porque os solutos iônicos sofrem o fenômeno da ionização ou dissociação, o que não ocorre com os moleculares. Assim, quando ionizam ou dissociam, o número de partículas na solução sempre será elevado.

Vejamos a seguir alguns passos fundamentais e exemplos de cálculo do número de partículas para soluções que apresentam cada um dos dois tipos de solutos.

Cálculo do número de partículas em uma solução com soluto molecular

A realização do cálculo do número de partículas em uma solução com um soluto molecular leva em consideração dois fatores fundamentais, a massa molar do soluto e a constante de Avogadro (6,02.10²³ partículas por mol).

Assim, quando conhecemos o soluto molecular e a massa que foi adicionada ao solvente, podemos calcular o número de partículas desse soluto realizando os seguintes passos:

1º Passo: Calcular a massa molar do soluto.

Para isso, basta multiplicar a massa do elemento pela quantidade de átomos dele na fórmula da substância e, em seguida, somar com os resultados dos outros elementos pertencentes à fórmula.

Exemplo: Cálculo da massa molar da sacarose (C₁₂H₂₂O₁₁), considerando que a massa atômica do C = 12 g/mol; massa atômica do H = 1 g/mol; e massa do O = 16 g/mol.

Massa molar = 12.12 + 1.22 + 11.16

Massa molar = 144 + 22 + 176

Massa molar = 342 g/mol

2º Passo: Montar a regra de três que determinará o número de partículas do soluto na solução.

Nessa regra de três, necessária para calcular o número de partículas da solução, na primeira linha, temos a massa molar e a constante de Avogadro. Na segunda linha, temos a incógnita e a massa do soluto que foi utilizado no preparo da solução.

Exemplo: Qual é o número de partículas em uma solução preparada pela adição de 50 g de sacarose em água?

1ª linha: 342 g-------------6,02.10²³ partículas

2ª linha: 50 g------------- x

342.x = 50.6,02.10²³

342x = 301.10²³

x = 301.10²³
     342

x = 0,88.10²³ partículas, aproximadamente

ou

x = 8,8.10²² partículas, aproximadamente

Cálculo do número de partículas em uma solução com soluto iônico

Para realizar o cálculo do número de partículas de solutos iônicos, devemos seguir o mesmo princípio utilizado no cálculo das soluções moleculares, ou seja, baseando-se na constante de Avogadro (6,02.10²³) e na massa molar.

Porém, não podemos esquecer que, quando dissolvido, o soluto iônico ioniza ou dissocia, liberando ou formando íons. Dessa forma, aumenta-se a quantidade de partículas presentes na solução. Essa observação foi realizada pelo químico Van't Hoff, o qual criou um fator para corrigir o número de partículas de um soluto iônico nesse tipo de solução.

Representação da ionização e dissociação de dois solutos diferentes

Ao multiplicar o número de partículas encontrado pela constante de Avogadro e pela massa molar, o fator de correção de Van't Hoff (representado por i) pode obter a real quantidade de partículas (íons) do soluto presente na solução.

A fórmula utilizada para a determinação do fator de correção de Van't Hoff é:

i = 1 + α.(q-1)

Na qual:

• α = grau de ionização ou dissociação do soluto (sempre dado em porcentagem);

• q = número de cátions e ânions presentes na fórmula da substância (por exemplo, na fórmula NaCl, temos um cátion e um ânion, logo q é igual a 2).

Exemplo: Qual é o número de partículas em uma solução preparada pela adição de 90 g de cloreto de cálcio em água?

1º Passo: Cálculo da massa molar do cloreto de cálcio (CaCl₂), considerando que a massa atômica do Ca = 40 g/mol e a massa do Cl = 35,5 g/mol, e que a solução apresenta um grau de dissociação de 40%.

Massa molar = 1.40 + 2.35,5

Massa molar = 40 + 71

Massa molar = 111 g/mol

2º Passo: Montar a regra de três para determinar o número de partículas do soluto na solução.

Nessa regra de três, como foi dito anteriormente, na primeira linha, estão a massa molar e a constante de Avogadro e, na segunda linha, temos a incógnita e a massa do soluto que foi utilizado no preparo da solução.

1ª linha: 111 g-------------6,02.10²³ partículas

2ª linha: 90 g------------- x

111.x = 90.6,02.10²³

111x = 541,8.10²³

x = 541,8.10²³
    111

x = 4,88.10²³ partículas, aproximadamente

3º Passo: Cálculo do fator de correção de Van't Hoff.

Para isso, devemos levar em consideração que o grau de dissociação (α) do soluto é de 40%, e que, na fórmula da substância, temos a presença de 1 cátion (apenas um de Ca) e 2 ânions (2 de Cl), o que resulta em um q igual a 3. Assim:

i = 1 + α.(q-1)

i = 1 + 0,4.(3-1)

i = 1 + 0,4.(2)

i = 1 + 0,8

i = 1,8

4º Passo: Encontrar o número real (y) de partículas do soluto iônico presentes na solução.

Para isso, devemos apenas multiplicar o número de partículas do segundo passo pelo fator de correção encontrado no terceiro passo.

y = 4,88.10²³.1,8

y = 8,784.10²³ partículas