Volume da esfera

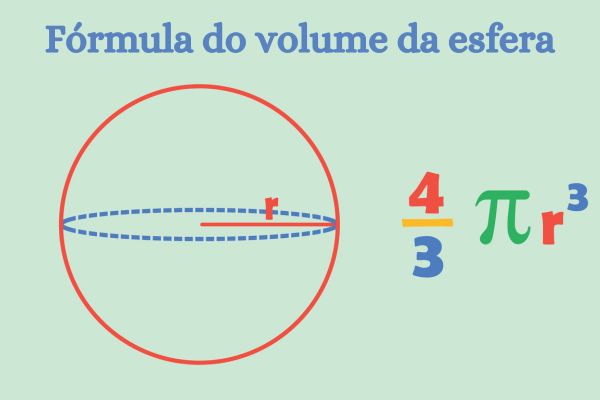
O volume da esfera é calculado pelo produto entre quatro terço de π vezes o cubo da medida do raio da esfera. Sendo assim, para calculá-lo, é necessário conhecer a medida do raio da esfera.

A esfera é um sólido geométrico, e os seus principais elementos são o raio, o centro, o diâmetro e a superfície. Já as regiões mais importantes desse sólido são a calota esférica, o fuso esférico e a cunha esférica.

Leia também: Como calcular o volume da pirâmide

Tópicos deste artigo

• 1 - Resumo sobre o volume da esfera
• 2 - Videoaula sobre o volume da esfera
• 3 - O que é uma esfera?
• 4 - Elementos da esfera
• 5 - Fórmula do volume da esfera
• 6 - Cálculo do volume da esfera
• 7 - Regiões da esfera
• 8 - Exercícios resolvidos sobre esfera

Resumo sobre o volume da esfera

• A esfera é um sólido geométrico que se assemelha a uma bola perfeita, em que todos os pontos da superfície estão à mesma distância de um ponto central, chamado centro.
• Os elementos da esfera são o centro, o raio, o diâmetro e a superfície.
• O volume da esfera é uma medida que quantifica o espaço ocupado por essa figura geométrica.
• A fórmula para calcular o volume da esfera é \( V=\frac{4}{3}\pi r^3\).
• Para calcular o volume, substituímos o valor de r pelo comprimento do raio e, quando necessário, o valor de π  por uma aproximação.
• A esfera possui regiões importantes, como a calota esférica, a cunha esférica e o fuso esférico.

Videoaula sobre o volume da esfera

O que é uma esfera?

A esfera é uma figura geométrica tridimensional em que todos os pontos de sua superfície estão igualmente distantes de um ponto central, denominado centro da esfera. De modo geral, a esfera é o sólido geométrico formado por todos os pontos que estão a uma distância menor ou igual a r.

Elementos da esfera

A esfera tem algumas partes importantes e, para compreender o cálculo do seu volume, é fundamental conhecer esses elementos.

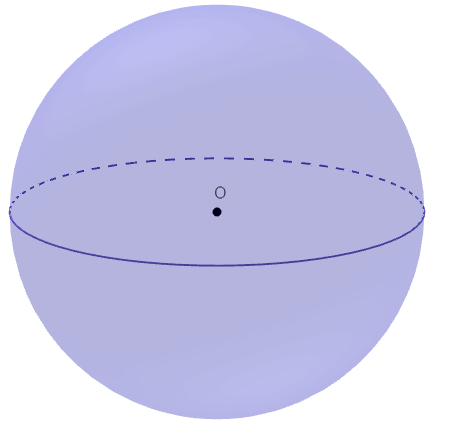
• Centro da esfera: o ponto equidistante de todos os pontos da superfície da esfera, o que significa que a distância do centro a qualquer ponto na superfície é sempre a mesma. O centro da esfera é conhecido também como origem da esfera.

• Diâmetro: a maior distância entre dois pontos em uma figura esférica, passando pelo seu centro. No contexto de uma esfera, o diâmetro é a reta que liga dois pontos opostos em sua superfície, atravessando o centro da esfera.

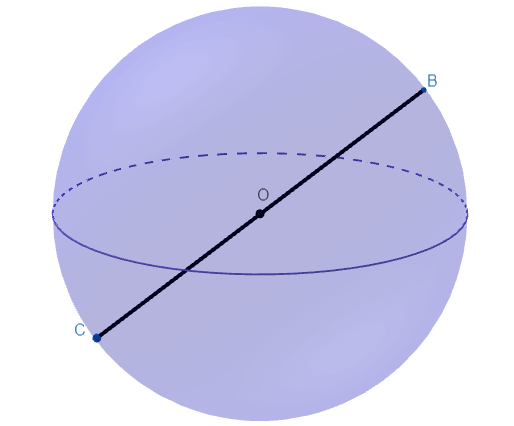
• Raio: a distância entre o centro de uma figura geométrica e qualquer ponto em sua superfície. Em outras palavras, o raio é a reta que liga o centro de um círculo ou de uma esfera a um ponto na sua borda.

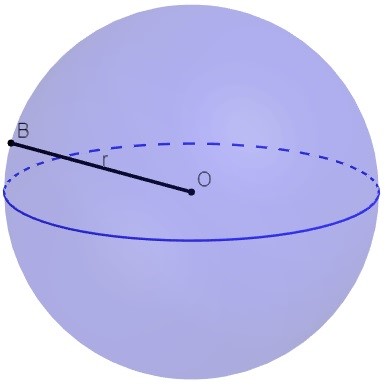
• Superfície esférica: a coleção de todos os pontos que estão equidistantes de um ponto central, conhecido como o centro da esfera. Para exemplificar, em uma bola, a superfície da esfera é a parte que tocamos.

Fórmula do volume da esfera

A fórmula abaixo é para o cálculo do volume da esfera:

\(V=\frac{4\pi R^3}{3} \) 

• V: volume da esfera;
• R: é o raio da esfera;
• π: é uma constante.

Cálculo do volume da esfera

Para calcular o volume da esfera, basta conhecer a medida do seu raio e, caso necessário, substituir o valor da constante π pela aproximação desejada.

Exemplo 1:

Qual é o volume de uma esfera que possui raio medindo 4 cm?

Resolução:

Sabemos que R = 4, então:

\(V=\frac{4\pi\cdot6^3}{3}\)

\(V=\frac{4\cdot\pi\cdot216}{3}\)

\(V=\frac{864\pi}{3}\)

\(V=288\pi\)

Exemplo 2:

Utilizando 3,1 como aproximação de π, qual é o volume de uma esfera que possui raio medindo 3 metros?

\(V=\frac{4⋅3,1⋅3^3}3\)

\(V=\frac{12,4\cdot27}{3}\)

\(V=12,4\ \cdot9\)

\(V=111,6\ m^3\)

Regiões da esfera

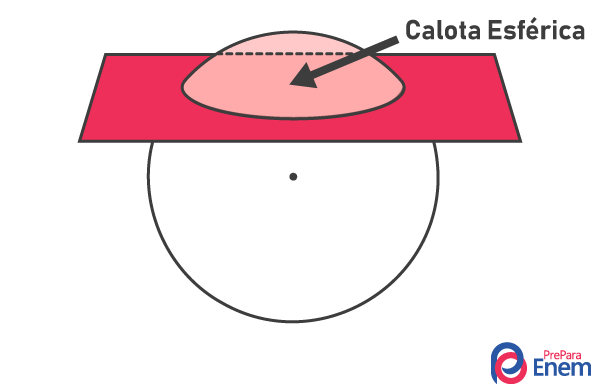
• Calota esférica: é o sólido geométrico formado quando dividimos a esfera por um plano.

​Fuso esférico: é a parte da superfície de uma esfera para um determinado ângulo.

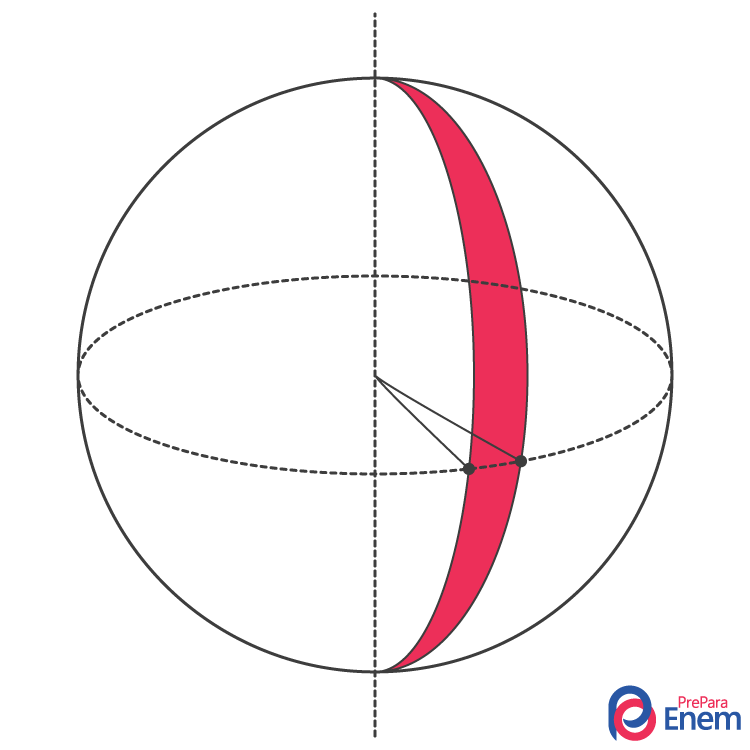
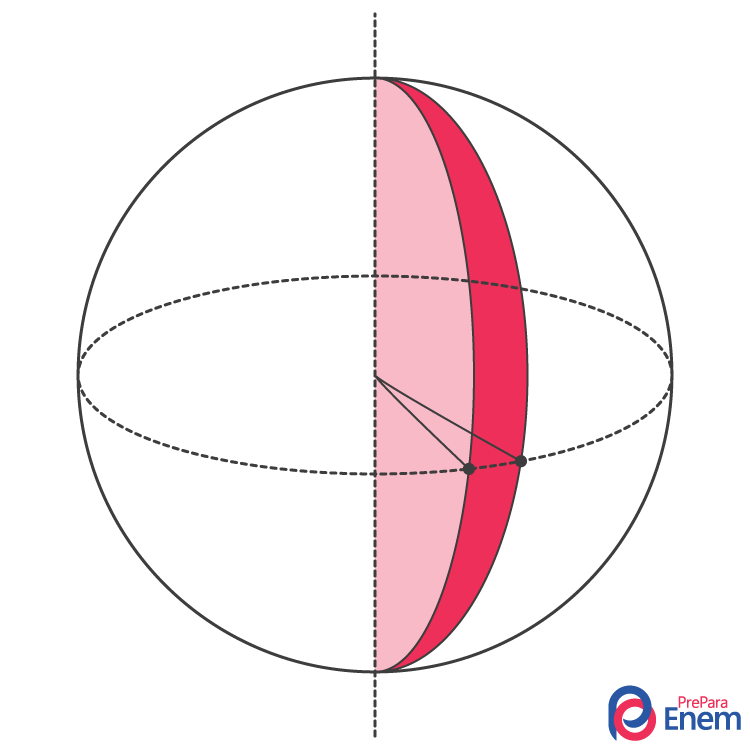
​Cunha esférica: A cunha esférica é o sólido geométrico formado por parte de uma esfera para um determinado ângulo.

​Outras fórmulas da esfera

• Raio: \(R=\frac{Diâmetro}2\)
• Área da superfície esférica: \(A=4\pi R^2\)
• Volume da cunha csférica: \(V_{cunha}=\frac{4\pi R^3}{3}\frac{\alpha}{360}\)

Vale dizer que α é o ângulo (em graus) de rotação do semicírculo.

Leia também: Corpos redondos — características, tipos e fórmulas

Exercícios resolvidos sobre esfera

Questão 1: Sabendo que o volume de uma esfera de raio X é 4 cm³, determine o volume de uma esfera de raio 2x.

A) 8cm³

B) 16cm³

C) 24cm³

D) 32cm³

E) 40cm³

Resolução:

Alternativa D.

Calculando o volume da esfera de raio x, temos que:

\(V=\frac{4\pi x^3}{3}\)

Calculando o volume da esfera de raio 2x, temos que:

\(V=\frac{4\pi{(2x)}^3}{3}=\frac{4\pi x^3}{3}⸳8\)

Dos resultados acima, concluímos que o volume da esfera de raio 2x é 8 vezes o volume da esfera de raio x. Logo, esse volume é \(V=8\cdot4=32{cm}^3\).

Questão 2: Se o diâmetro de uma esfera é 20 cm, determine o volume da esfera. Adote π=3 .

A) 1000cm³

B) 2000cm³

C) 3000cm³

D) 4000cm³

E) 5000cm³

Resolução:

Alternativa D.

O raio da esfera é a metade do diâmetro, logo o raio é 10 cm.

O volume da esfera é dado por \(V=\frac{4\pi R^3}{3}\).

Substituindo esse valor, temos \(V=\frac{4⸳3⸳10^3}3=4000cm^3\).

Fontes:

SILVA, João. Geometria Esférica: Fundamentos e Aplicações. São Paulo: Editora ABC, 2022.

BOULOS, Paulo; CAMARGO, Ivan. Geometria Analítica. São Paulo: Editora XYZ.