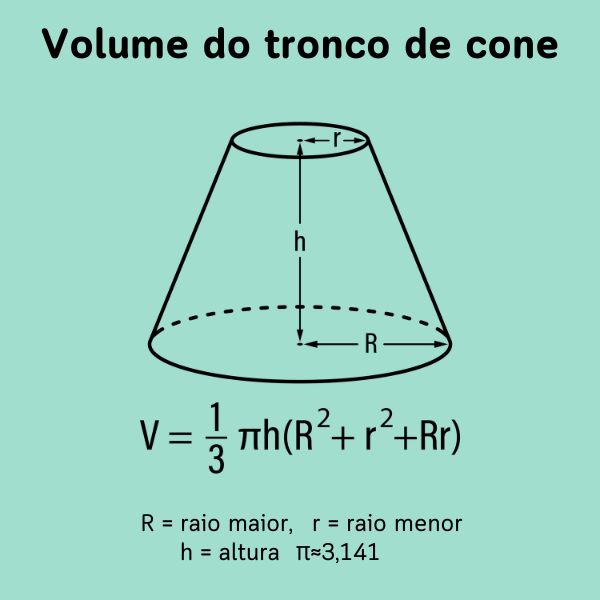
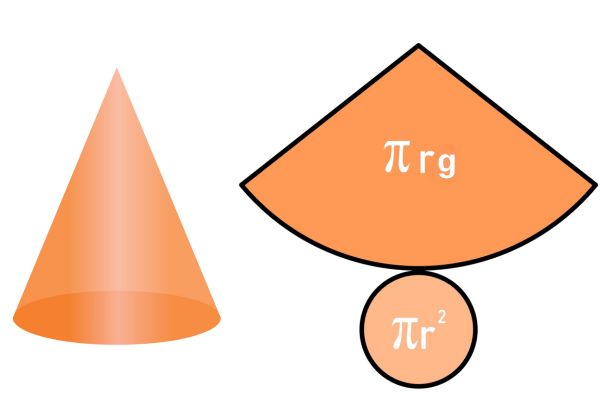
O cone é um dos sólidos geométricos com bastante aplicação no cotidiano. Diversas embalagens, produtos e até reservatórios apresentam a forma de um cone circular reto. Em virtude da sua grande utilização, é necessário conhecer seus elementos e fórmulas para o cálculo de sua área e volume. Vejamos o que é necessário para obter o volume de um cone de revolução.
Considere um cone circular reto de altura h e raio r como mostra a figura.

Assim como na pirâmide, o volume do cone é dado em função da área de sua base e da altura h. Podemos pensar no cone como sendo uma pirâmide com uma das faces arredondadas. Logo, seu volume pode ser obtido fazendo:
![]()
Como a base do cone é uma circunferência de raio r, temos que:
![]()
Assim, a fórmula para o cálculo do volume do cone pode ser reescrita da seguinte forma:
![]()
Onde,
r → é a medida do raio da base
h → é a altura do cone
V → é o volume do cone
Observe que para obter o volume do cone não é necessário conhecer a medida da geratriz e a fórmula é semelhante à da pirâmide.
Vejamos alguns exemplos de aplicação da fórmula.
Exemplo 1. Calcule o volume de um cone circular reto de 13 cm de altura e raio da base medindo 6 cm. (Use π = 3,14)
Solução: Pelo enunciado do problema, temos que:
r = 6 cm
h = 13 cm
V = ?
Utilizando a fórmula do volume, obtemos:

Portanto, o cone apresenta um volume de 489,84 cm3.
Exemplo 2. Um reservatório de água possui a forma de um cone de revolução com 8 metros de profundidade. Sabendo que o diâmetro da base mede 4 metros, determine a capacidade, em litros, desse reservatório. (Use π = 3,14)

Solução:
Segundo o enunciado do problema, temos que:
h = 8 m (profundidade)
r = d/2 = 4/2 = 2 m
Determinar a capacidade é o mesmo que calcular o volume do reservatório. Assim, utilizando a fórmula do volume do cone, obtemos:

Como o problema deseja saber a capacidade do reservatório em litros, devemos lembrar da seguinte relação:
1 m3 = 1000 litros
Assim, a capacidade do reservatório será:
V = 33,49 ×1000 = 33490 litros
Videoaulas relacionadas: