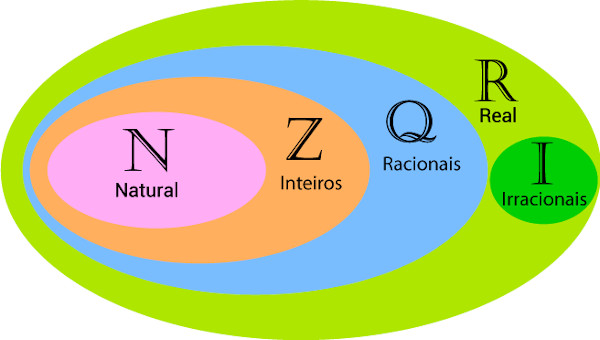
O número pi é representado pela letra grega π e é um dos mais importantes números irracionais conhecidos na Matemática. Um número é irracional quando a sua representação decimal é uma dízima não periódica, e o número π é um desses casos, pois o seu valor é de aproximadamente 3,14159265358979323846...
O número π foi encontrado durante os estudos sobre a circunferência. Foi percebido que o comprimento da circunferência era um pouco mais que 3 diâmetros da circunferência. Nessa tentativa de descobrir a relação entre o comprimento da circunferência e o seu diâmetro, é que foram encontrados valores cada vez mais próximos da constante π.
Leia também: Números racionais — aqueles que podem ser escritos como uma fração
Tópicos deste artigo
- 1 - Resumo sobre o número π
- 2 - Qual é o valor de pi?
- 3 - Como calcular o valor de pi?
- 4 - Para o que o número pi serve?
- 5 - História do número pi
Resumo sobre o número π
- O número π (lê-se pi) é um número irracional, ou seja, uma dízima não periódica.
- O valor aproximado de π é 3,141592653...
- Ele é utilizado para calcular comprimento, área e volume de figuras geométricas arredondadas.
- Quando necessário, utilizamos aproximações para o valor de π , como 3,1 ou 3,14 ou 3,141.
Qual é o valor de pi?
O número π (lê-se: pi) é um número irracional, e possui um valor constante. Ele é representado por esse símbolo por ser uma dízima não periódica, ou seja, possui infinitas casas decimais, mas não um período. Na resolução de questões de Matemática, é bastante comum utilizarmos aproximações para o valor dessa constante, como 3,1; 3,14; 3,141; 3,1415.
O número de casas decimais que se precisa depende do que se procura calcular. Em experimentos de Física, por exemplo, costuma-se pegar mais casas decimais do π , pois, quanto maior o número de casas decimais, melhor será a precisão dos valores encontrados.
Atualmente, conhecemos várias casas decimais do número π , já foram apresentadas 62,8 trilhões delas. A seguir, representaremos somente as primeiras 500 casas decimais desse número, logo, temos que:
π= 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912.
Como calcular o valor de pi?
O número π foi encontrado quando se comparou o comprimento da circunferência com o seu diâmetro. Foi quando se percebeu que o comprimento correspondia a pouco mais que 3 vezes o diâmetro.
Ao tentar-se calcular a parte decimal desse número, encontrou-se sempre resultados que se aproximavam do que hoje é o valor de π .
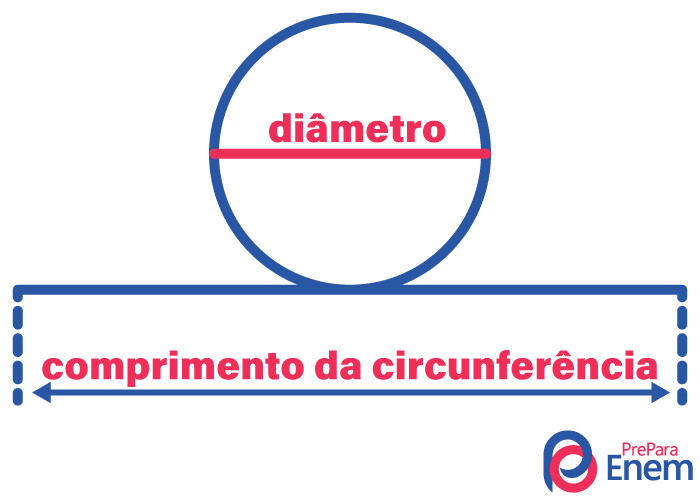
O número π é obtido quando se divide o comprimento da circunferência pelo diâmetro. Mas vale ressaltar que geralmente utiliza-se de aproximações para essas medidas, e, portanto, encontra-se aproximações de π ao fazer a divisão.
\(V=\frac{comprimento\ da\ circunferência}{diâmetro\ da \ circunferência}\)
Para o que o número pi serve?
O número π é utilizado para realizar cálculos envolvendo as figuras geométricas que possuem formas circulares e também os corpos redondos, como no cálculo da área e do comprimento de circunferências, arcos, elipses, e na área da face e no volume dos cones, cilindros esferas e demais sólidos geométricos.
Por exemplo, para calcular o comprimento da circunferência, utilizamos a fórmula:
\(C=2\pi r\)
Já a área é calculada por:
\(A=\pi r^2\)
O volume do cilindro é calculado por:
\(V=\pi r^2h\)
O volume do cone é:
\(V=\frac{\pi r^2h}{3}\)
Existem várias outras fórmulas que envolvem o π , sempre relacionadas a figuras arredondadas.
Leia também: Como se calcula a área de uma esfera?
História do número pi
A constante π foi uma descoberta humana realizada há muito tempo. É possível encontrar relatos de que os egípcios e os babilônicos já usavam aproximações para o valor de π , pois eles já sabiam que essa razão era de aproximadamente 3.
Com o passar dos anos, e o desenvolvimento da Matemática, outros estudiosos foram encontrando melhores aproximações de π. Euclides fez estudos relevantes sobre a constante que possibilitaram que Arquimedes conseguisse uma aproximação melhor do valor de π . Para encontrar essa aproximação, usou-se a comparação do perímetro de um polígono com o comprimento da circunferência. Arquimedes encontrou 3,142 como a melhor aproximação para π , utilizando o perímetro do hexágono para compará-lo com o da circunferência.
Ptolomeu, utilizando o mesmo método com um polígono de 720 lados, encontrou o valor de 3,1416. Esse valor posteriormente foi superado pelos chineses, que conseguiram encontrar π=3,14159 , usando um polígono de 3072 lados.
Foram desenvolvidos métodos diferentes para calcular a aproximação do valor de π , chegando a aproximações cada vez mais precisas dele. Com o passar do tempo, foi possível descobrir o valor de mais casas decimais. Com o uso da tecnologia, tornou-se possível alcançar o recorde atual, de 62,8 trilhões de casas decimais, calculado pela Universidade de Ciências Aplicadas de Grisons.