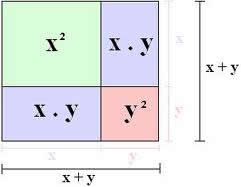
Os trinômios do tipo x2 + Sx + P podem ser escritos pela forma fatorada (x + a) * (x + b), pois temos:
(x + a) * (x + b) = x2 + xb + xa + ab = x2 + x(a + b) + ab
Observe que o termo ligado à incógnita x é originado pela soma de a com b e o termo constante é resultado da multiplicação de a por b. Portanto, todas as multiplicações envolvendo (x + a) * (x + b) são representadas pela expressão x² + Sx + P.
No trinômio x2 + 2x – 24, temos que a forma fatorada é dada pela expressão (x + 6) * (x – 4), pois:
Soma = 6 – 4 = 2
Produto = 6 * (–4) = –24
Veja mais exemplos:
x2 + 4x – 21 = (x + 7) * (x – 3)
Soma = 7 – 3 = 4
Produto = 7 * (–3) = – 21
x2 – 9x + 20 = (x – 4) * (x – 5)
Soma = – 4 – 5 = – 9
Produto = (–4) * (–5) = 20
x2 + x – 72 = (x + 9) * (x – 8)
Soma = 9 – 8 = 1
Produto = 9 * (–8) = – 72
x2 + 13x + 22 = (x + 2) * (x + 11)
Soma = 2 + 11 = 13
Produto = 2 * 11 = 22