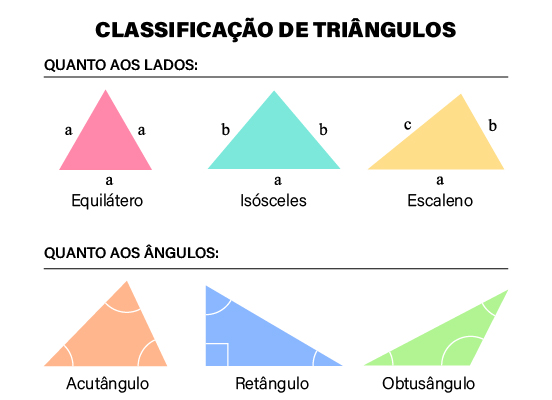
Conhecemos como triângulo isósceles um triângulo que possui dois lados congruentes e um lado não congruente. Analisando os lados de um triângulo, existem três classificações possíveis. Ele pode ser:
-
equilátero, quando todos os lados são congruentes;
-
escaleno, quando nenhum lado é congruente; ou
-
isósceles, quando dois lados são congruentes.
Em um triângulo isósceles, o lado que possui medida diferente é conhecido como base, e os outros lados são chamados de oblíquos. Existem propriedades importantes para esse tipo de figura, como os ângulos da base também serem congruentes, e a altura relativa à base ser também a mediana da base e a bissetriz.
Para calcular a área e o perímetro do triângulo isósceles, utilizamos a mesma fórmula usada para calcular a área e o perímetro de um triângulo qualquer.
Leia também: Qual é a condição de existência de um triângulo?

Tópicos deste artigo
- 1 - Triângulo isósceles
- 2 - Propriedades do triângulo isósceles
- 3 - Área do triângulo isósceles
- 4 - Perímetro do triângulo isósceles
- 5 - Exercícios resolvidos
Triângulo isósceles
O triângulo é um polígono que possui três lados e é estudado na geometria plana. Quando essa figura geométrica possui exatamente dois lados congruentes, ela é conhecido como triângulo isósceles.
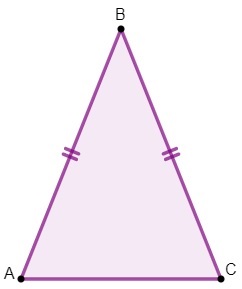
No triângulo ABC, temos que:
-
os lados AB e BC são congruentes;
-
o lado AC é a base do triângulo isósceles;
-
o ponto B é o vértice do triângulo;
-
os ângulos A e C são os ângulos da base e o ângulo B é o ângulo do vértice.
Propriedades do triângulo isósceles
Existem propriedades específicas do triângulo isósceles, as quais resultam dos dois lados congruentes.
-
1ª propriedade: os ângulos da base de um triângulo isósceles são congruentes.
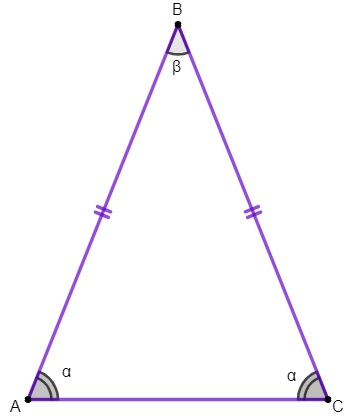
Aplicaremos essa propriedade para encontrar o valor dos ângulos internos de um triângulo isósceles.
Exemplo:
Encontre o valor dos ângulos da base de um triângulo isósceles sabendo que o ângulo do seu vértice mede 50º.
Sabemos que a soma dos ângulos de um triângulo qualquer é sempre igual a 180º e que os ângulos da base do triângulos isósceles são congruentes. Então, seja x a medida de um deles, temos que:
x + x + 50 = 180
2x = 180 – 50
2x = 130
x = 130 : 2
x = 65º
-
2ª propriedade: a altura da base é também a mediana da base e a bissetriz do vértice do triângulo.
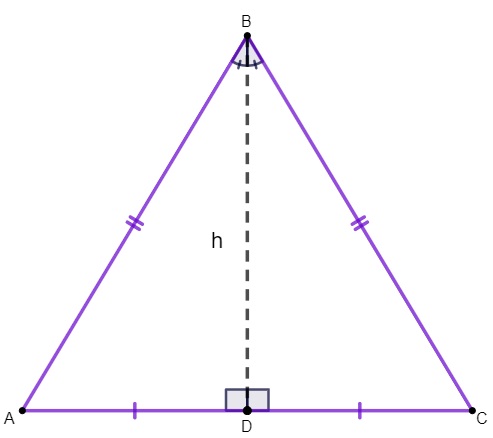
Como consequência dessa propriedade, temos que:
⇒ segmentos AD e AC são congruentes;
⇒ ângulos ABD e CBD são congruentes.
-
3ª propriedade: eixo de simetria.
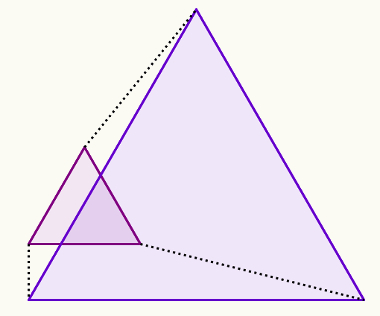
Note que, se traçarmos a altura, estaremos dividindo o triângulo em dois triângulos semelhantes:
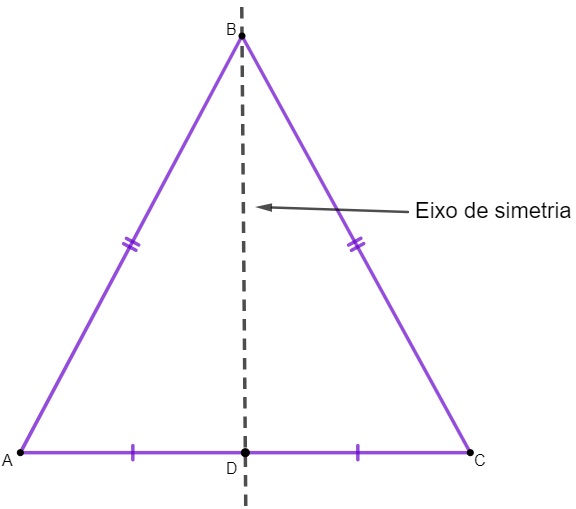
Perceba que o eixo de simetria divide a figura em outros dois triângulos simétricos.
Leia também: 3 macetes de Matemática para o Enem
Área do triângulo isósceles
Para calcular a área do triângulo isósceles, utilizamos a mesma fórmula que é utilizada para calcular a área de um triângulo qualquer. A diferença é que, em alguns casos, é possível encontrar a altura ou o tamanho da base utilizando uma das propriedades do triângulo.
Sendo assim, a área do triângulo isósceles é dada por:
![]()
Exemplo:
Calcule a área do triângulo isósceles a seguir.
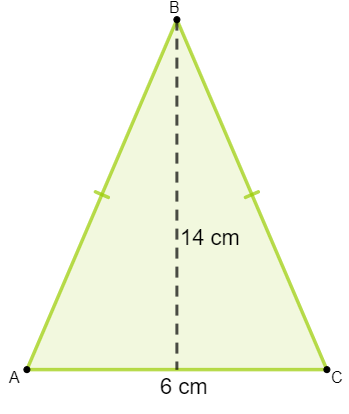
A sua altura apresenta 14 cm e sua base possui 6 cm, então:
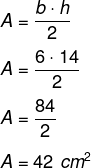
Perímetro do triângulo isósceles
Para calcular o perímetro de um triângulo isósceles, basta realizar a soma dos seus lados.
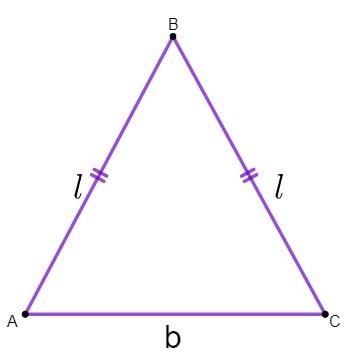
Como dois lados são congruentes, o perímetro do triângulo isósceles pode ser calculado por:
|
P = 2l + b |
Exemplo:
Em um triângulo isósceles, o seu lado oblíquo mede 13 metros, e a sua base, 24 metros. Calcule o seu perímetro.
P = 2l + b
P = 2 · 13 + 24
P = 26 + 24
P = 50 metros
Leia também: Quais são os casos de congruência de triângulos?
Exercícios resolvidos
Questão 1 - Sabendo que o triângulo a seguir possui os lados medidos em centímetros, a área dele é igual a:
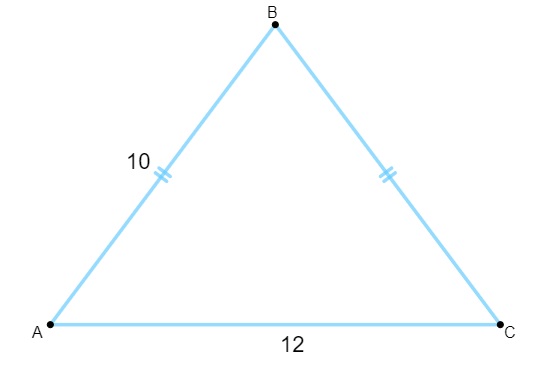
A) 120 cm².
B) 96 cm².
C) 80 cm².
D) 48 cm².
E) 30 cm².
Resolução
Alternativa D.
Para calcular a área, precisamos encontrar o valor da altura. Sabendo que a altura do triângulo isósceles é a mediana da base, temos que:
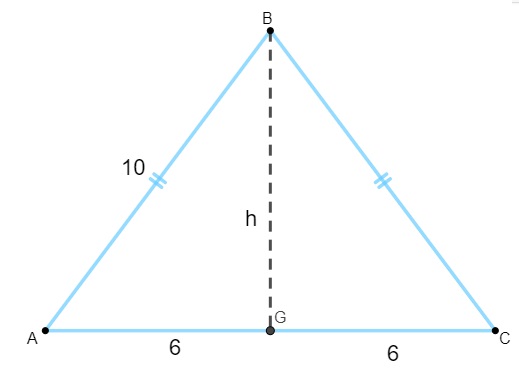
Note que o triângulo AGB é retângulo, então aplicaremos o teorema de Pitágoras para calcular a sua altura:
10² = 6² + h²
100 = 36 + h²
100 – 36 = h²
64 = h²
h² = 64
h = √64
h = 8
Como a altura é 8 e a base é 12, temos que:
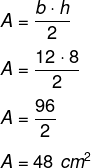
Questão 2 - (Cefet-SC 2008) Num triângulo isósceles, cada ângulo da base mede o dobro da medida do ângulo do vértice. A medida do ângulo do vértice é:
A) 36°.
B) 72°.
C) 50°.
D) 40°.
E) 80°.
Resolução
Alternativa A.
Seja x o ângulo do vértice, então os ângulos da base medem 2x cada. Sabemos que a soma dos ângulos internos de um triângulo é 180º, então:
x + 2x + 2x = 180º
5x = 180º
x = 180º : 5
x = 36º