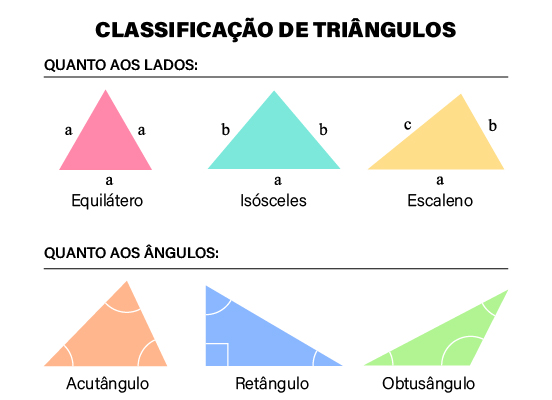
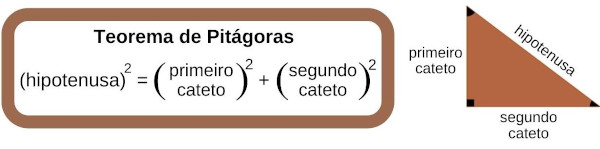
A classificação dos triângulos é utilizada para identificar características em comum entre essas figuras bem como desenvolver o estudo de suas propriedades específicas. Há duas maneiras diferentes de se classificar um triângulo, a primeira leva em consideração os lados dele e a segunda, os ângulos.
Quando classificamos o triângulo levando em consideração os lados, ele pode ser: equilátero, quando todos os lados têm mesma medida; isósceles, quando dois lados têm mesma medida; ou escaleno, quando as medidas dos lados são todas distintas.
Quando classificamos o triângulo levando em consideração os ângulos, ele pode ser: obtuso, quando tem um ângulo interno obtuso; reto, quando tem um ângulo interno reto; ou agudo, quando tem todos os ângulos internos agudos.
Leia também: Quais são os pontos notáveis de um triângulo?
Tópicos deste artigo
- 1 - Resumo sobre classificação de triângulos
- 2 - Videoaula sobre classificação de triângulos
- 3 - Como são classificados os triângulos?
- 4 - Tipos de triângulos em relação à medida dos lados
- 5 - Tipos de triângulos em relação ao ângulo
- 6 - Propriedades dos triângulos
- 7 - Exercícios resolvidos sobre classificação de triângulos
Resumo sobre classificação de triângulos
- A classificação dos triângulos é utilizada para identificar características comuns e estudar as propriedades dessas figuras.
- Há duas maneiras de se classificar triângulos: pela medida dos lados ou pela medida dos ângulos.
- Quando classificamos levando em consideração os lados, o triângulo pode ser:
- equilátero: todos os lados com mesma medida;
- isósceles: dois lados com mesma medida;
- escaleno: todos os lados com medidas diferentes.
- Quando classificamos levando em consideração os ângulos, o triângulo pode ser:
- obtuso: tem um ângulo obtuso;
- reto: tem um ângulo reto;
- agudo: todos os ângulos são agudos.
Videoaula sobre classificação de triângulos
Como são classificados os triângulos?
Os triângulos podem ser classificados de duas formas independentes, considerando características diferentes. A primeira forma leva em conta os comprimentos dos lados, classificando-os em:
- escaleno;
- equilátero;
- isósceles.
A segunda forma leva em consideração a medida dos ângulos internos, classificando os triângulos em:
- obtusângulo;
- acutângulo;
- retângulo.
Essas classificações ajudam a identificar propriedades específicas e a compreender melhor as características dos triângulos.
Tipos de triângulos em relação à medida dos lados
Quando comparamos a medida dos lados de um triângulo, podemos encontrar três casos distintos:
- O triângulo pode ter as medidas dos lados todas congruentes.
- O triângulo pode ter dois lados com a mesma medida.
- O triângulo pode ter todos os lados com medidas distintas.
Cada um desses casos recebe nomes específicos, apresentados a seguir.
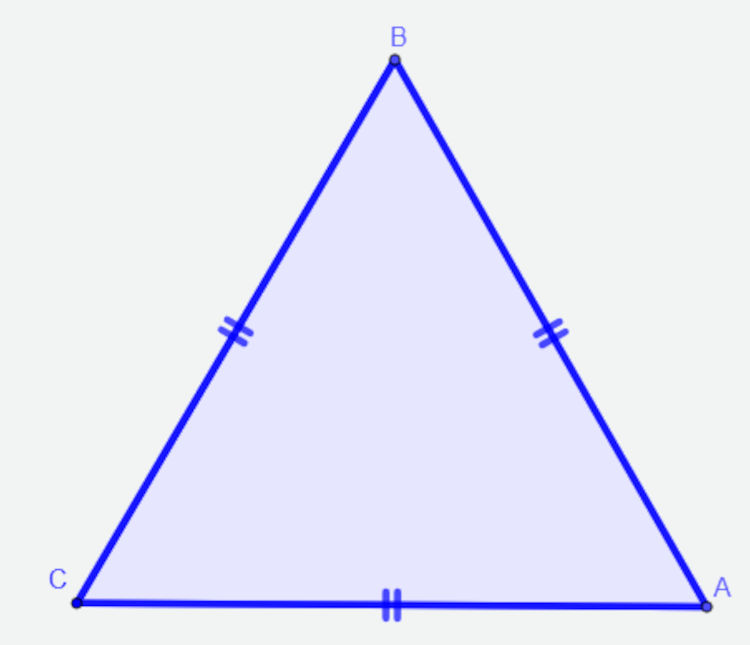
→ Triângulo equilátero
O triângulo é equilátero quando ele tem todos os lados com medidas congruentes, ou seja, os lados do triângulo têm as mesmas medidas.
-
Propriedade específica do triângulo equilátero
Pelo fato de ter todos os lados com a mesma medida, para calcular a área do triângulo equilátero e a altura, existe uma fórmula específica válida somente para ele. Vamos considerar como l a medida do lado do triângulo, então a altura do triângulo equilátero pode ser calculada por:
\(h=\frac{l\sqrt3}{2}\)
Já a área do triângulo equilátero pode ser calculada por:
\(A=\frac{l^2\sqrt3}{4}\)
|
Observação: Como os lados do triângulo equilátero são iguais, os ângulos internos também serão iguais; cada ângulo interno do triângulo equilátero mede 60º. |
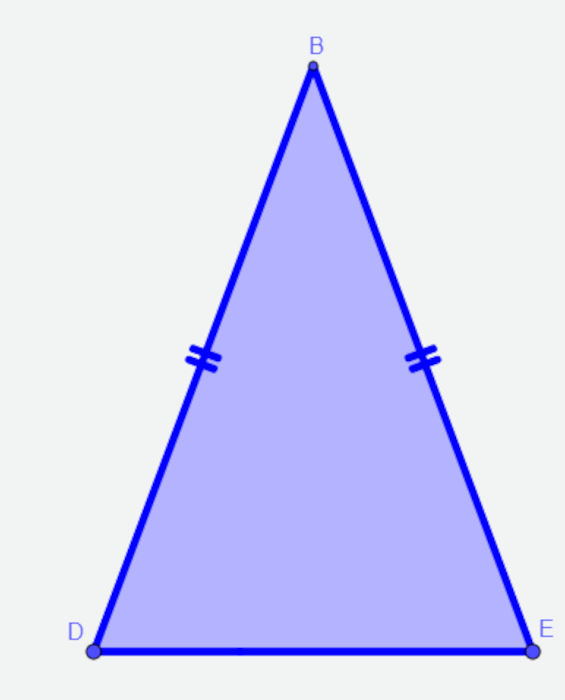
→ Triângulo isósceles
O triângulo é isósceles quando tem dois lados com medidas congruentes, ou seja, dois lados do triângulo têm o mesmo comprimento, enquanto o terceiro lado tem uma medida diferente.
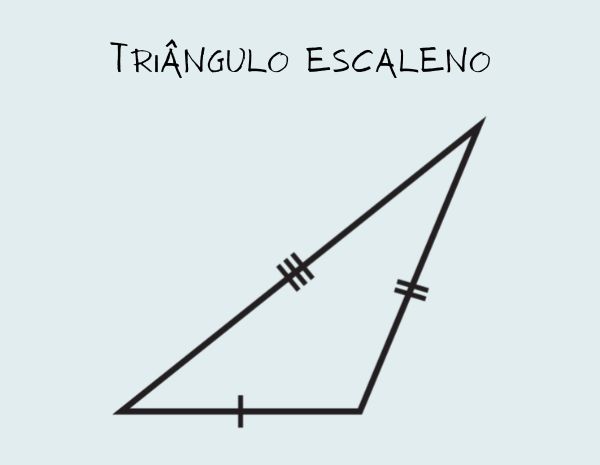
→ Triângulo escaleno
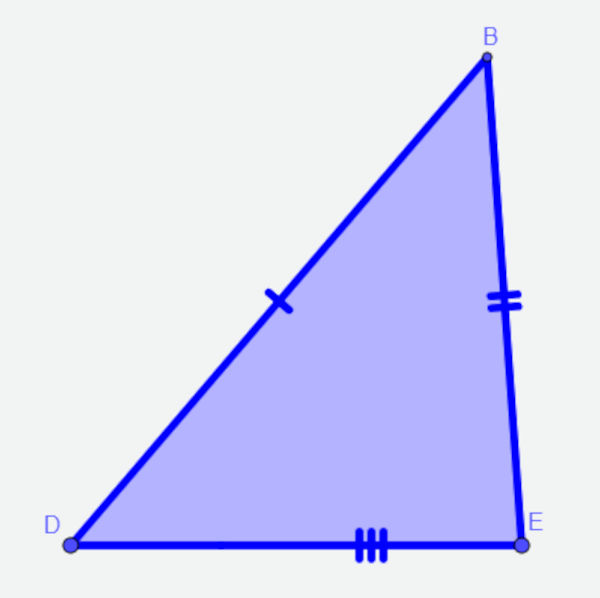
O triângulo é escaleno quando todos os seus lados têm medidas diferentes, ou seja, nenhum dos seu lados tem comprimento igual ao do outro.
Veja também: Como identificar semelhanças entre triângulos?
Tipos de triângulos em relação ao ângulo
Quando analisamos a medida dos ângulos internos de um triângulo, podemos classificá-lo em três tipos distintos. O triângulo pode ter todos os ângulos menores que 90°, pode apresentar um ângulo igual a 90°, ou, ainda, pode ter um ângulo maior que 90°. Cada um desses casos recebe um nome específico, conforme descrito a seguir.
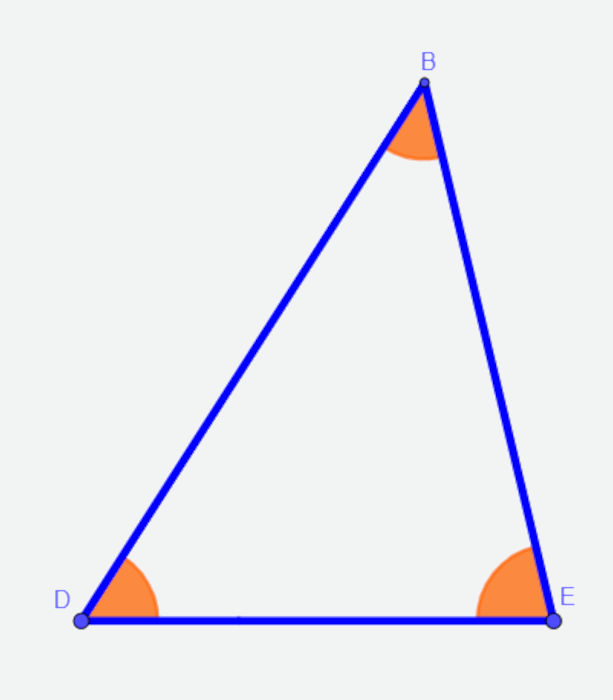
→ Triângulo acutângulo
O triângulo é acutângulo quando todos os seus ângulos internos são menores que 90°, ou seja, todos os ângulos são agudos.
→ Triângulo retângulo
O triângulo é retângulo quando tem um ângulo interno reto, com exatamente 90°, enquanto os outros dois ângulos são agudos.
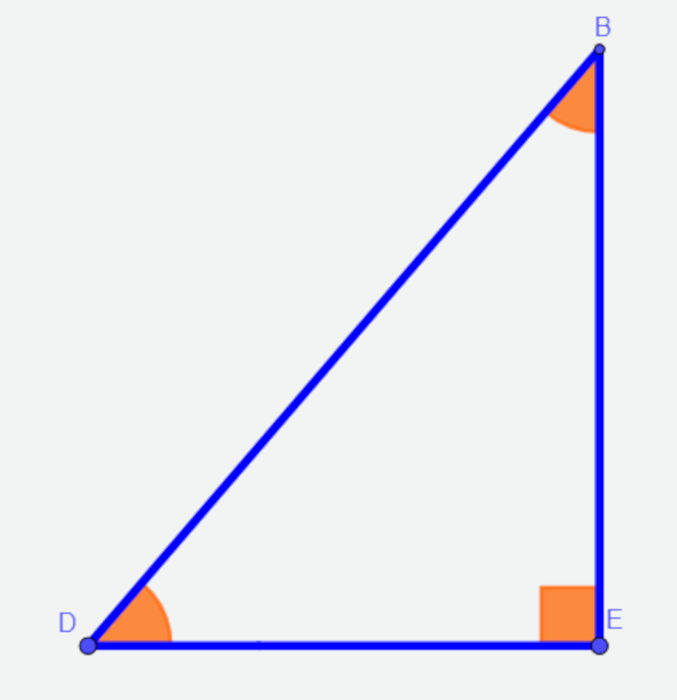
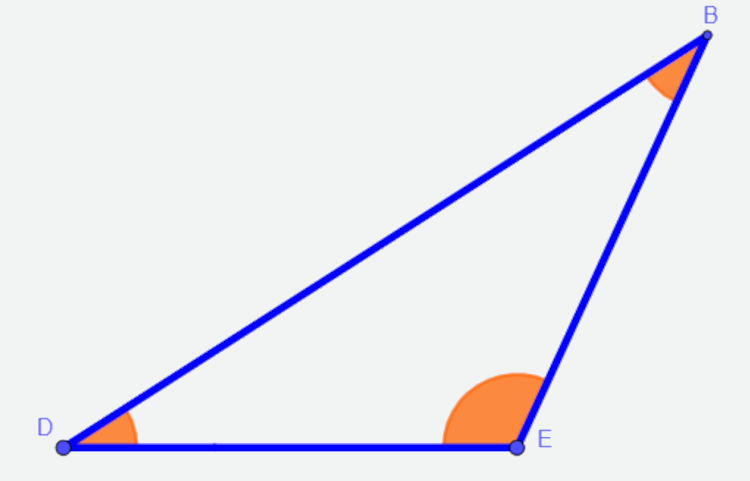
→ Triângulo obtusângulo
O triângulo é obtusângulo quando tem um ângulo interno maior que 90°, ou seja, um ângulo obtuso, enquanto os outros dois ângulos são agudos.
Propriedades dos triângulos
Nos triângulos existem propriedades comuns válidas para todos os tipos de triângulos, são elas:
- O triângulo não tem diagonal.
- A soma dos ângulos internos de um triângulo é sempre igual a 180º.
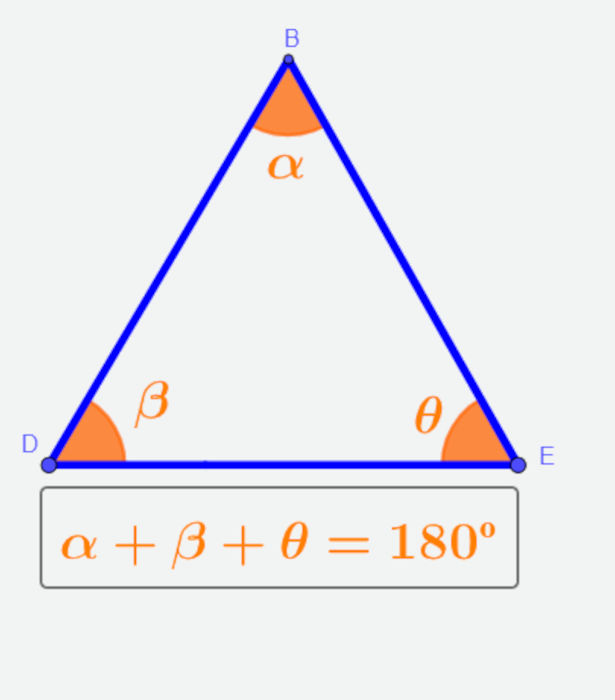
- A soma dos ângulos externos do triângulo é sempre igual a 360º.
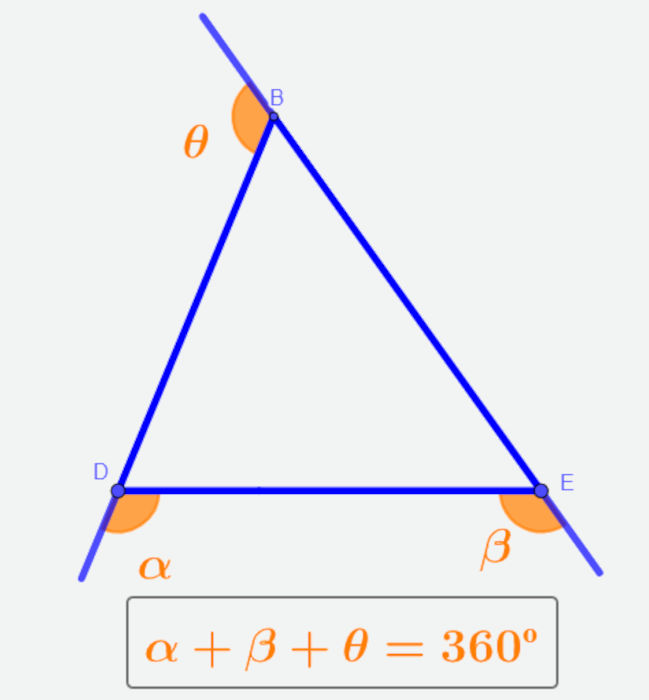
- A soma de dois lados de um triângulo será sempre maior que o seu terceiro lado.
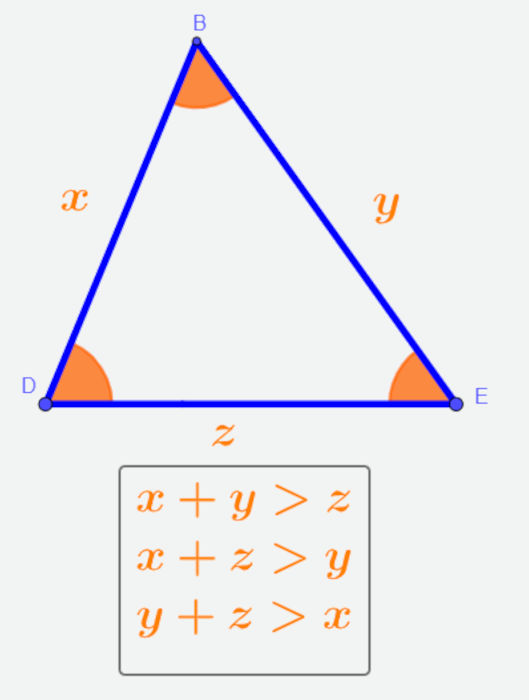
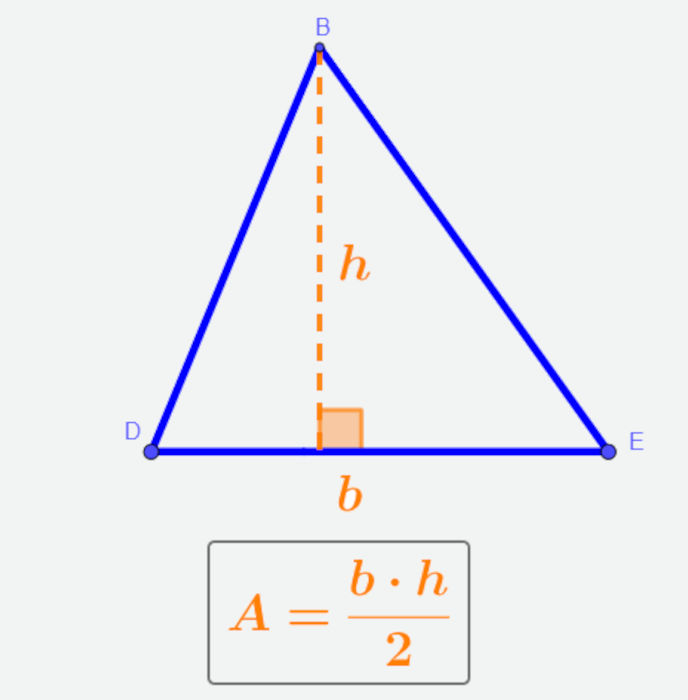
- A área do triângulo é igual ao produto entre a base e a altura divido por dois.
Saiba mais: Como é feita a classificação dos quadrados
Exercícios resolvidos sobre classificação de triângulos
Questão 1
Durante o planejamento da construção de um parque ecológico, um engenheiro ambiental identificou que a área delimitada no mapa tinha o formato de um triângulo com ângulos medindo 90° 60° e 30°. Sobre esse triângulo, é correto afirmar que ele é:
A) obtusângulo
B) acutângulo
C) retângulo
D) equilátero
E) isósceles
Resolução:
Alternativa C
Como o triângulo tem um ângulo de 90º, ou seja, um ângulo reto, então esse triângulo é retângulo.
Questão 2
Um triângulo pode ser classificado quanto aos ângulos. Analise as seguintes afirmativas:
I. Todo triângulo equilátero é acutângulo.
II. Um triângulo retângulo tem dois ângulos agudos.
III. Um triângulo obtusângulo pode ter dois ângulos obtusos.
Marque a alternativa correta:
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas são verdadeiras.
Resolução
Alternativa C
I. Todo triângulo equilátero é acutângulo:
Verdadeiro. Em um triângulo equilátero, todos os ângulos medem 60°, são ângulos agudos.
II. Um triângulo retângulo tem dois ângulos agudos:
Verdadeiro. Em um triângulo retângulo, há um ângulo reto (90°) e os outros dois ângulos devem ser agudos, pois a soma dos ângulos internos é sempre 180°.
III. Um triângulo obtusângulo pode ter dois ângulos obtusos:
Falso. Um triângulo pode ter, no máximo, um ângulo obtuso (maior que 90°), pois a soma dos ângulos internos é 180º.
Fontes
DANTE, Luiz Roberto. Matemática: contexto e aplicações. Volume 3. 3. ed. São Paulo: Ática, 2011.
GIOVANNI, José Ruy; CASTRUCCI, Benedito; GIOVANNI JR, José Ruy. A Conquista da Matemática. Volume 3. 10. ed. São Paulo: FTD, 2014.