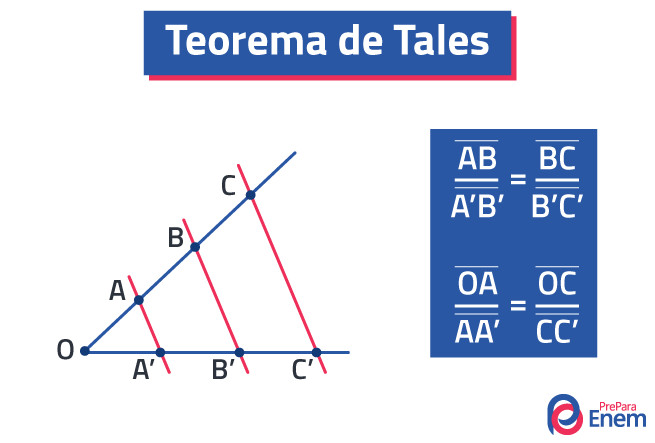
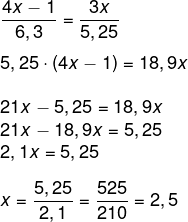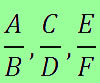O teorema de Tales é aplicado na geometria plana e demonstra que há proporcionalidade em um feixe de retas paralelas cortadas por retas transversais a elas. Ele foi demonstrado pelo matemático Tales de Mileto, que provou essa proporcionalidade entre os segmentos de reta formados entre retas paralelas e retas transversais. A partir dessa relação de proporção, é possível descobrir o valor desses segmentos, tornando o teorema de Tales uma ferramenta importante para o cálculo de medidas.
Tópicos deste artigo
- 1 - Enunciado do teorema de Tales
- 2 - Como se resolve o teorema de Tales?
- 3 - Teorema de Tales em triângulos
- 4 - Exercícios resolvidos
Enunciado do teorema de Tales
O teorema de Tales foi desenvolvido pelo matemático Tales de Mileto e pode ser aplicado a diversas situações da geometria. Ele é utilizado para auxiliar no encontro de medidas desconhecidas. O enunciado do teorema de Tales diz o seguinte:
Dado um feixe de retas paralelas, há segmentos proporcionais sobre duas ou mais retas transversais.
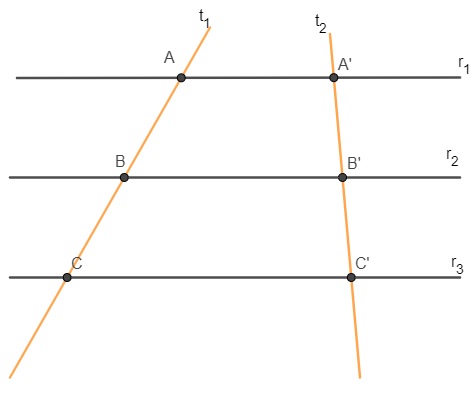
As retas r1 r2 e r3 são paralelas, e as retas t1 e t2 são transversais. Então, pelo teorema de Tales, temos que:
![]()
Como se resolve o teorema de Tales?
Utilizamos o teorema de Tales para encontrar valores desconhecidos quando existem retas paralelas e retas transversais com segmentos proporcionais. Para isso, é necessário conhecer a medida de pelo menos três segmentos de reta. Vamos analisar um exemplo em que é possível utilizar o teorema de Tales para encontrar a medida de um dos segmentos.
Exemplo 1:
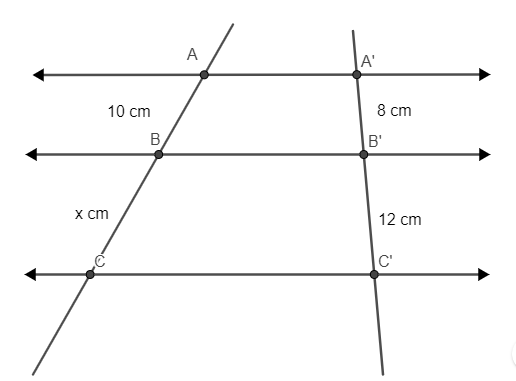
Para encontrar o valor de x, é necessário montar as proporções. Sabemos que o segmento formado pelos pontos A e B está para o segmento formado pelos pontos B e C, assim como o segmento formado pelos pontos A’ e B’ está para o segmento formado pelos pontos B’ e C’.
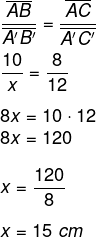
Exemplo 2:
Encontre o valor de y sabendo que AC = 10 cm.
Sabemos que AC está para BC, assim como A’C’ está para B’C’. Note que o comprimento do segmento A’C’ é 4 + 6 = 10 cm. Montando a proporção, chegamos a:
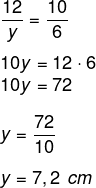
Veja também: Ponto de intersecção entre duas retas concorrentes
Teorema de Tales em triângulos
Uma aplicação interessante para o teorema de Tales é o seu uso em triângulos. Quando traçamos segmentos proporcionais à base do triângulo, estamos, na verdade, construindo um triângulo menor semelhante ao triângulo maior. Como eles são semelhantes, consequentemente os lados são proporcionais, o que torna o teorema de Tales uma ferramenta importante para encontrar o comprimento do lado desses triângulos.
Exemplo 1:
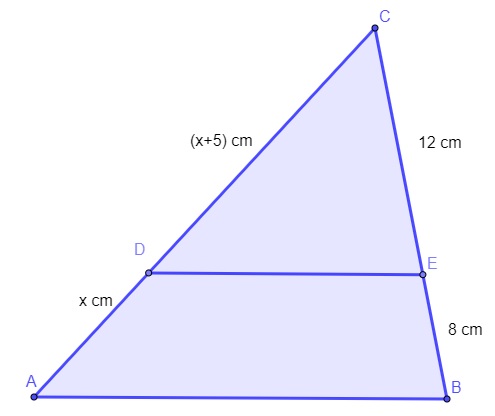
Sabendo que o segmento DE é paralelo a AB, encontre o valor de x.
Aplicando o teorema de Tales, temos que:
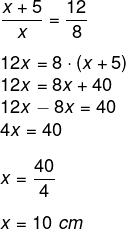
Veja também: Quais são as condições de existência de um triângulo?
Exercícios resolvidos
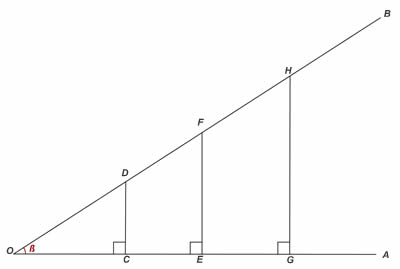
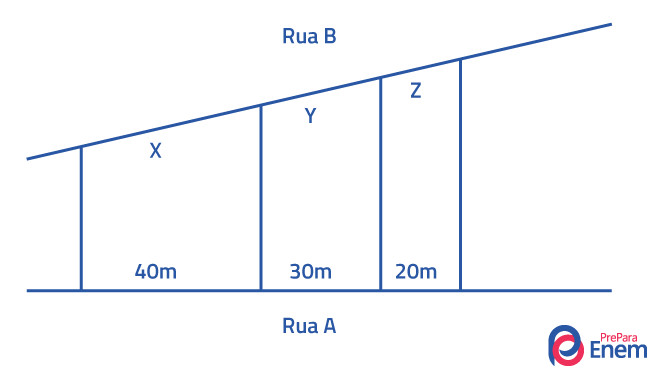
Questão 1 – (Fuvest — adaptada) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de x, y e z em metros, respectivamente, sabendo que a frente total para essa rua tem 180 m?
A) 90, 60 e 30.
B) 80, 60 e 40.
C) 40, 60 e 90.
D) 20, 30 e 40.
Resolução
Alternativa B.
O comprimento da frente dos terrenos (x + y + z) é igual a 180 m, e o comprimento na rua A é igual a 40 + 30 + 20 = 90 m.
Aplicando o teorema de Tales, temos que:
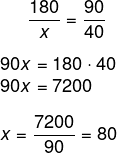
Utilizando o mesmo raciocínio, vamos encontrar o valor de y e de z:
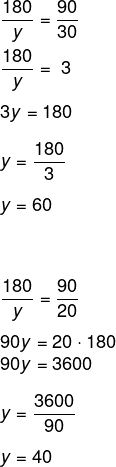
Questão 2 – Na figura a seguir, as retas r, s e t são paralelas.
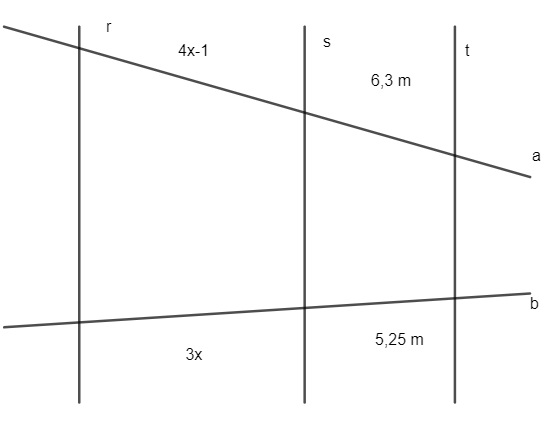
O valor de x, em metros, é:
A) 1,5.
B) 2,0.
C) 2,5.
D) 3,0.
E) 4,5.
Resolução
Alternativa C.
Aplicando o teorema de Tales, temos que: