A tabuada é uma organização em forma de tabela das quatro operações básicas: adição, subtração, multiplicação e divisão. O objetivo desse formato é facilitar a visualização das operações entre números naturais e auxiliar a aprendizagem.
Estudar a tabuada significa se familiarizar com os números e com os tipos mais simples de contas. Com o tempo, conforme lidamos com a Matemática em nosso dia a dia, o uso das operações se torna natural. Assim, ao contrário do que se acredita, não é necessário memorizar completamente a tabuada, mas sim entender seu funcionamento.
Leia também: Dicas para o cálculo da multiplicação
Tabuada da adição
A tabuada da adição consiste em organizar as somas entre os números.
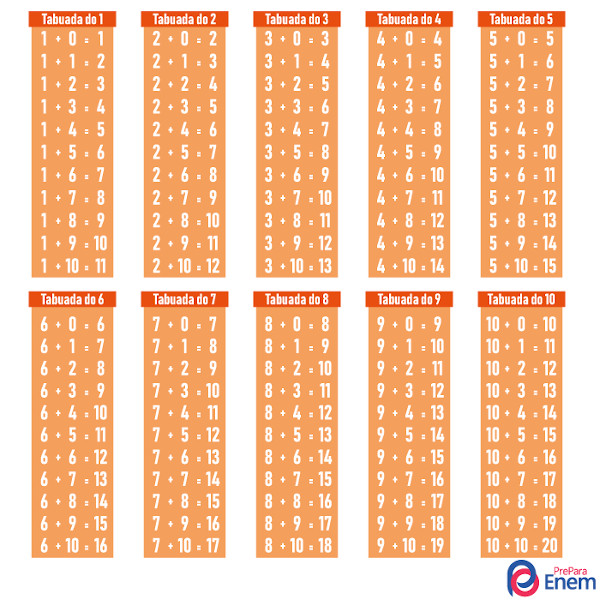
Tabuada da subtração
A tabuada da subtração corresponde à lista das diferenças positivas entre os números.
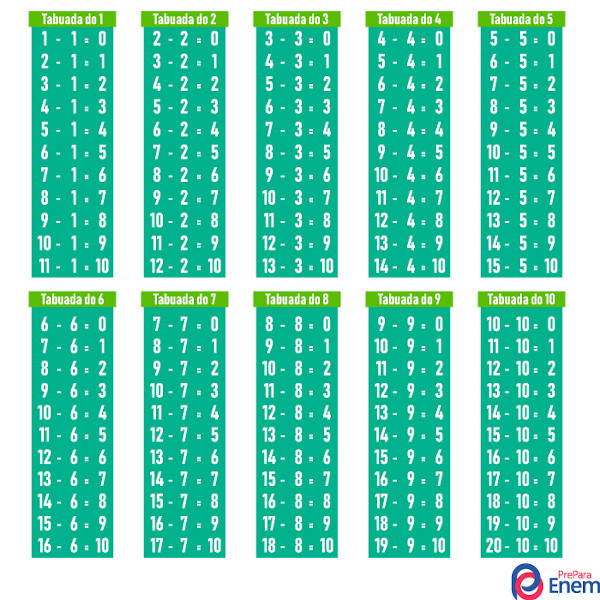
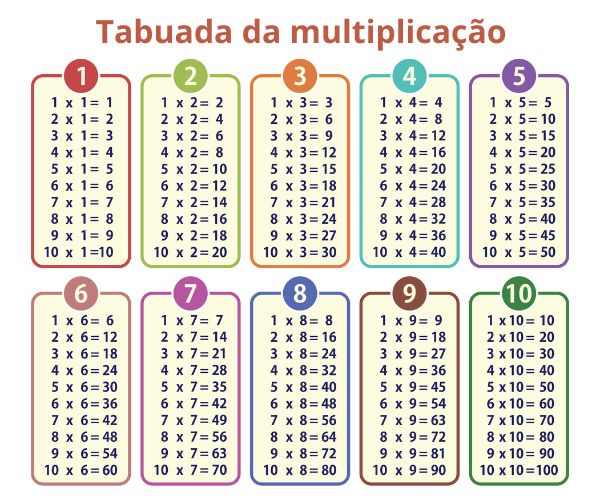
Tabuada da multiplicação
A tabuada da multiplicação é a mais importante das tabuadas. Ela abrange os produtos entre os números.
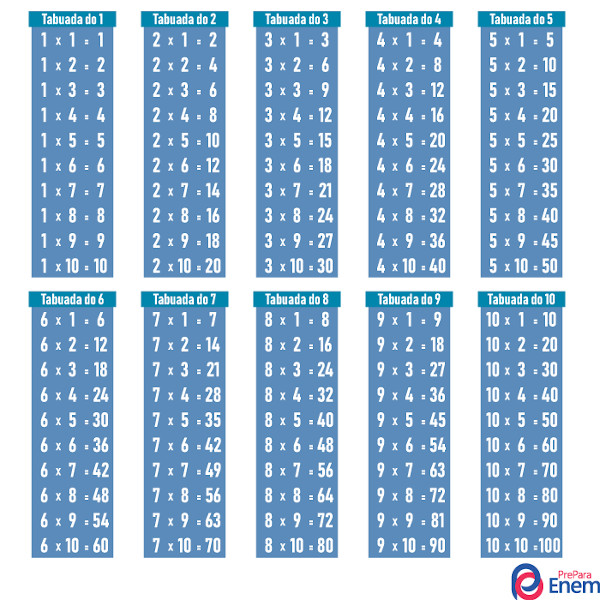
-
Como fazer a tabuada cartesiana?
A tabuada cartesiana, também conhecida como tabuada de Pitágoras, é uma maneira de escrever a tabuada da multiplicação. Para representá-la, construímos uma tabela com os números de 1 a 10 dispostos na horizontal e na vertical, além de um x no topo esquerdo. No local de encontro desses números, escrevemos o resultado da multiplicação entre eles.
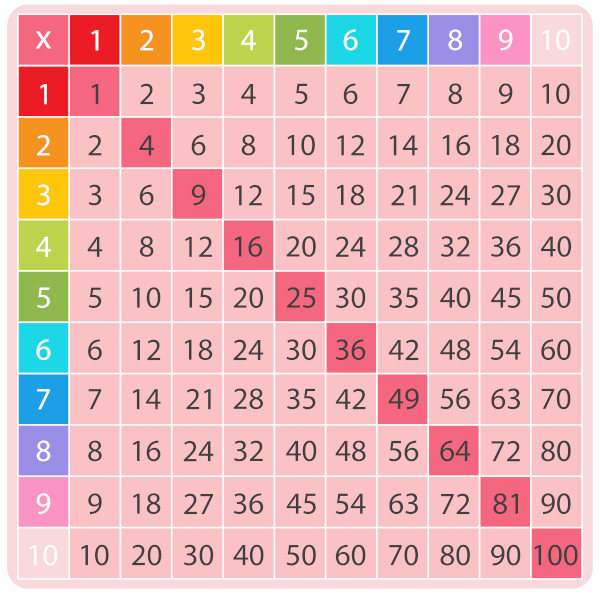
Tópicos deste artigo
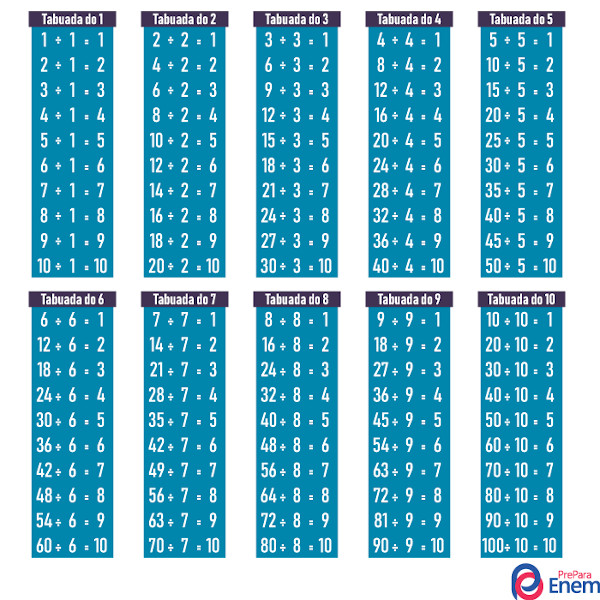
Tabuada da divisão
A tabuada da divisão apresenta a razão (ou quociente) entre os números.
Dicas de como aprender a tabuada
As tabuadas envolvem as quatro operações fundamentais entre números naturais: adição, subtração, multiplicação e divisão. Portanto, duas dicas fundamentais para aprender qualquer uma das tabuadas são entender as relações entre essas quatro operações e investigar suas propriedades.
1. Relações entre as quatro operações
As quatro operações básicas estão relacionadas de diferentes maneiras. A multiplicação, por exemplo, é a adição entre parcelas iguais: 5 x 4 é 4 + 4 + 4 + 4 + 4. Assim, se conhecemos a adição, podemos aprender a multiplicação.
No caso do estudo da tabuada, a ideia é muito semelhante: podemos aproveitar o conhecimento sobre uma operação para fazer deduções sobre a outra.
A operação de subtração é inversa à operação de adição, por exemplo, pois realiza o processo contrário. Acompanhe os exemplos a seguir, em que utilizamos a subtração para reverter o que foi feito pela adição.
Exemplos:
a) 2 + 3 = 6 e 6 – 3 = 2
b) 5 + 7 = 12 e 12 – 7 = 5
c) 9 + 1 = 10 e 10 – 1 = 9
A operação de divisão é inversa à operação de multiplicação. Analise os exemplos abaixo, nos quais a divisão é utilizada para desfazer o processo de multiplicação.
Exemplos:
a) 3 x 4 = 12 e 12 ÷ 4 = 3
b) 6 x 5 = 30 e 30 ÷ 5 = 6
c) 8 x 2 = 16 e 16 ÷ 2 = 8
2. Propriedades
Para o estudo das tabuadas, as propriedades mais importantes das quatro operações são a propriedade comutativa e a do elemento neutro.
- Comutativa: na adição e multiplicação, a ordem das parcelas não altera o resultado.
Exemplos:
a) 6 + 7 = 13 e 7 + 6 = 13
b) 2 x 9 = 18 e 9 x 2 = 18
Cuidado! Essa propriedade não é válida para as operações de subtração e divisão.
a) 4 – 3 = 1, mas 3 – 4 = – 1
b) 10 ÷ 5 = 2, mas 5 ÷ 10 = 0,5
- Elemento neutro: para as quatro operações, há um número que não influencia no resultado, ou seja, é um elemento neutro.
Na adição e subtração, esse número é o 0, conforme os exemplos a) e b) (respectivamente) a seguir. Já na multiplicação e divisão, o elemento neutro é o 1, como indicado nos itens c) e d).
Exemplos:
a) 3 + 0 = 3
b) 8 – 0 = 8
c) 7 x 1 = 7
d) 6 ÷ 1 = 6
Leia também: Jogo de sinais — a análise do sinal do resultado de operações matemáticas
Exercícios resolvidos sobre a tabuada
Questão 1
Qual alternativa contém os números que completam, de cima para baixo, a tabuada a seguir?

a) 4, 1, 40, 2, 32.
b) 3, 40, 4, 1, 48.
c) 4, 3, 40, 2, 48.
d) 3, 4, 48, 2, 40.
e) 1, 2, 40, 3, 48.
Solução:
Alternativa C
Observe que neste exercício é interessante conhecer a propriedade comutativa da multiplicação e utilizá-la com seus conhecimentos sobre a tabuada do 8. Além disso, aplicando a propriedade do elemento neutro da multiplicação, é possível eliminar as alternativas a), b) e e). Já a alternativa d) pode ser eliminada com o uso da operação reversa da multiplicação, por exemplo, na segunda conta.
Questão 2
Considere os itens I a IV a seguir e identifique quais sinais devem ser utilizados (+, –, x ou ÷) no lugar do ponto de interrogação para torná-las verdadeiras:
I. 9 ? 1 = 9
II. 8 ? 2 = 16
III. 0 ? 8 = 8
IV. 10 ? 5 = 2
Solução:
Neste exercício, uma possível estratégia é testar todas as operações para cada conta ou realizar cálculos mentais. Também vale observar que os itens I e III envolvem elementos nulos. Usando esses raciocínios, podemos encontrar as operações corretas:
I. Permite duas respostas: 9 x 1 = 9 ou 9 ÷ 1 = 9.
II. 8 x 2 = 16
III. 0 + 8 = 8
IV. 10 ÷ 5 = 2