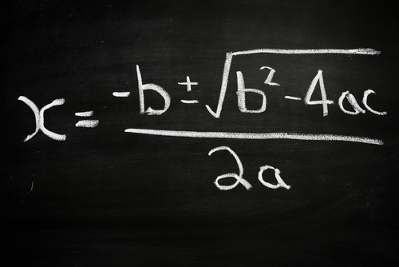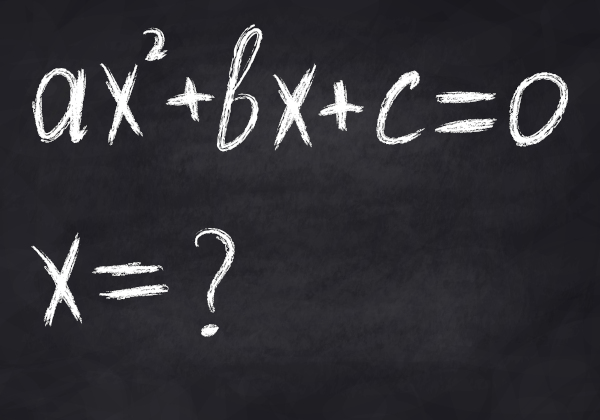Soma e produto é um método de resolução de equações polinomiais do 2° grau que relaciona os coeficientes da equação com a soma e o produto de suas raízes. A aplicação desse método consiste em tentar determinar quais são os valores das raízes que satisfazem certa igualdade entre expressões.
Mesmo se tratando de uma alternativa à fórmula de Bhaskara, esse método nem sempre pode ser utilizado, e, em algumas vezes, tentar encontrar os valores das raízes pode ser uma tarefa demorada e complexa, necessitando-se recorrer à tradicional fórmula de resolução de equações do 2° grau.
Leia também: Como resolver equações do segundo grau incompletas?
Tópicos deste artigo
- 1 - Resumo sobre soma e produto
- 2 - Fórmulas de soma e produto
- 3 - Cálculo das raízes usando soma e produto
Resumo sobre soma e produto
-
Soma e produto é um método alternativo para resolução de equações do 2° grau.
-
A fórmula da soma é \(-\frac{a}b\), enquanto a fórmula do produto é \(\frac{c}a\).
-
Esse método só pode ser utilizado se a equação possui raízes reais.
Fórmulas de soma e produto
Uma equação polinomial do segundo grau é representada da seguinte forma:
\(ax^2+bx+c=0\)
Em que o coeficiente \(a≠0\).
Resolver essa equação é o mesmo que encontrar quais são as raízes \(x_1\) e \(x_2\) que fazem a igualdade ser verdadeira. Assim, pela fórmula de Bhaskara, sabe-se que essas raízes podem ser expressas por:
\(x_1=\frac{-b + \sqrtΔ}{2a}\) e \(x_2=\frac{-b - \sqrtΔ}{2a}\)
Em que \(Δ=b^2-4ac\).
Portanto, as relações de soma e de produto são dadas por:
-
Fórmula da soma
\(x_1+x_2=\frac{-b+\sqrt∆}{2a}+\frac{-b-\sqrt∆}{2a}\)
\(x_1+x_2=-\frac{b}a\)
-
Fórmula do produto
\(x_1 ⋅ x_2=\frac{-b+\sqrt∆}{2a}\cdot \frac{-b-\sqrt∆}{2a}\)
\(x_1⋅x_2=\frac{c}a\)
Cálculo das raízes usando soma e produto
Antes de aplicar esse método, é importante saber se de fato é possível e viável utilizá-lo, ou seja, é preciso saber se a equação a ser resolvida possui raízes reais ou não. Caso a equação não possua raízes reais, ele não pode ser utilizado.
Para descobrir essa informação, pode-se calcular o discriminante da equação, pois este determina quantas soluções reais a equação do 2° grau tem:
Se Δ > 0, a equação possui duas raízes reais diferentes.
Se Δ = 0, a equação possui duas raízes reais e iguais.
Se Δ < 0, a equação não possui raízes reais.
Vejamos, a seguir, alguns exemplos de como aplicar o método de soma e produto.
-
Exemplo 1: Utilizando o método da soma e produto, se possível, calcule as raízes da equação \(-3x^2+4x-2=0\).
Primeiramente, é recomendável analisar se essa equação possui raízes reais ou não.
Calculando seu discriminante, tem-se que:
\(b^2 -4ac=(4)^2-4⋅(-3)⋅(-2)\)
\(= 16-24=-9\)
Portanto, as raízes da equação são complexas e não é possível utilizar esse método para encontrar o valor delas.
-
Exemplo 2: Usando o método de soma e produto, encontre as raízes da equação \(x^2+3x-4=0\).
Para saber se as raízes da equação são reais, calcula-se novamente seu discriminante:
\(b^2 -4ac =(3)^2-4⋅(1)⋅(-4)\)
\(=9+16=25\)
Assim, como o discriminante deu um valor maior que zero, pode-se afirmar que essa equação possui duas raízes reais distintas, e o método de soma e produto pode ser utilizado.
Pelas fórmulas deduzidas, sabe-se que as raízes \(x_1 \) e \(x_2\) cumprem as relações:
\(x_1+x_2=-\frac{3}1=-3\)
\(x_1⋅x_2=\frac{-4}1=-4\)
Portanto, a soma das duas raízes resulta em \(-3 \) e o produto delas resulta em \(-4 \).
Analisando o produto das raízes, percebe-se que uma delas é um número negativo e a outra é um número positivo, afinal, sua multiplicação resultou em um número negativo. Podemos então testar algumas possibilidades:
\(1⋅(-4)=-4\)
\(2⋅(-2)=-4\)
\((-1)⋅4=-4\)
Perceba que, das possibilidades levantadas, a primeira resulta na soma que se deseja obter, afinal:
\(1+(-4)=-3\).
Logo, as raízes dessa equação são \(x_1=1\) e \(x_2=-4\).
-
Exemplo 3: Usando o método da soma e produto, encontre as raízes da equação \(-x^2+4x-4=0\).
Calculando o discriminante:
\(b^2 -4ac=(4)^2-4⋅(-1)⋅(-4)\)
\(=16-16=0\)
Conclui-se que essa equação possui duas raízes reais e iguais.
Assim, utilizando as relações de soma e produto, temos que:
\(x_1+x_2=-\frac{4}{(-1)}=4\)
\(x_1⋅x_2=\frac{-4}{-1}=4\)
Portanto, o número real que cumpre as condições acima é o 2, pois \(2+2=4\) e \(2⋅2=4\), sendo então \(x_1=x_2=2\) as raízes da equação.
-
Exemplo 4: Encontre as raízes da equação \(6x^2+13x+6=0\).
Calculando o discriminante:
\(b^2-4ac=(13)^2 -4⋅(6)⋅(6)\)
\(=169-144=25\)
Conclui-se que essa equação possui duas raízes reais e diferentes.
Assim, utilizando as relações de soma e produto, temos que:
\(x_1+x_2=-\frac{13}6\)
\(x_1⋅x_2=\frac{6}6=1\)
Perceba que a fórmula da soma originou um resultado fracionário. Assim, encontrar o valor das raízes por esse método, mesmo sendo possível, pode se tornar algo demorado e trabalhoso.
Nesses casos, utilizar a fórmula de Bhaskara é uma estratégia melhor, e, assim, por meio de seu uso, pode-se encontrar as raízes da equação, que, nesse caso, são dadas por:
\(x_1=\frac{-b+ \sqrtΔ}{2a}=\frac{-13+ \sqrt{25}}{12}=-\frac{2}3\)
\(x_2=\frac{-b- \sqrtΔ}{2a}=\frac{-13- \sqrt{25}}{12}=-\frac{3}2\)
Leia também: Método de completar quadrados — outra alternativa à fórmula de Bhaskara
Exercícios resolvidos sobre soma e produto
Questão 1
Considere uma equação polinomial do 2° grau do tipo \(ax^2+bx+c=0\) (com \(a=-1\)) , cuja soma das raízes é igual a 6 e o produto das raízes é igual a 3. Qual das equações a seguir cumpre essas condições?
a) \(-x^2-12x-6=0\)
b) \(-x^2-12x+6=0\)
c) \(-x^2+6x-3=0\)
d) \(-x^2-6x+3=0\)
Resolução: letra C
O enunciado informa que a soma das raízes da equação é igual a 6 e o produto delas é igual a 3, ou seja:
\(x_1+x_2=-\frac{b}a=6\)
\(x_1⋅x_2=\frac{c}a=3\)
Sabendo disso, podemos isolar os coeficientes b e c em função do coeficiente a , isto é:
\(b=-6a\ ;\ c=3a\)
Por fim, como o coeficiente \(a=-1\), conclui-se que \(b=6\) e \(c=-3\).
Questão 2
Considere a equação \(x^2+18x-36=0\). Denotando por S a soma das raízes dessa equação e por P o produto delas, podemos afirmar que:
a) \(2P=S\)
b) \(-2P=S\)
c) \(P=2S\)
d) \(P=-2S\)
Resolução: letra C
Pelas fórmulas de soma e produto, sabemos que:
\(S=-\frac{b}a=-18\)
\(P=\frac{c}a=-36\)
Portanto, como \(-36=2\cdot (-18)\), segue que \(P=2S\).
Fontes:
LEZZI, Gelson. Fundamentos de matemática elementar, 6: complexos, polinômios, equações. 8. ed. São Paulo: Atual, 2013.
SAMPAIO, Fausto Arnaud. Trilhas da matemática, 9º ano: ensino fundamental, anos finais. 1. ed. São Paulo: Saraiva, 2018.