Através de uma demonstração simples, podemos constatar que a soma das medidas dos ângulos internos de um triângulo equivale a 180o. O mesmo pode ser feito para os demais polígonos convexos. Sabendo o número de lados de um polígono, conseguimos determinar a soma das medidas de seus ângulos internos.
Um quadrilátero pode ser dividido em dois triângulos, portanto a soma das medidas de seus ângulos internos é:
S = 2?180O = 360O
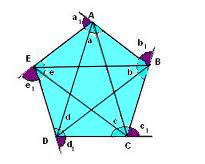
Um pentágono pode ser dividido em três triângulos, logo, a soma das medidas de seus ângulos internos é:
S = 3?180O = 540O
Partindo da mesma ideia, um hexágono pode ser dividido em 4 triângulos. Assim, a soma das medidas de seus ângulos internos é:
S = 4?180O = 720O
Generalizando, se um polígono convexo possui n lados, a soma das medidas de seus ângulos internos será dada por:
S = (n - 2)?180o
Exemplo 1. Determine a soma das medidas dos ângulos internos de um icoságono.
Solução: Icoságono é um polígono convexo com 20 lados, logo, n = 20. Assim, teremos:
S = (n - 2)?180o
S = (20 - 2)?180o
S = 18?180o
S = 3240o
Exemplo 2. Quantos lados possui um polígono cuja soma das medidas dos ângulos internos é igual a 1440o?
Solução: Sabemos que S = 1440o e queremos determinar a quantidade de lados que esse polígono possui, ou seja, determinar o valor de n. Vamos resolver o problema utilizando a fórmula da soma dos ângulos internos.

Portanto, o polígono cuja soma dos ângulos internos é igual a 1440o é o decágono, que apresenta 10 lados.
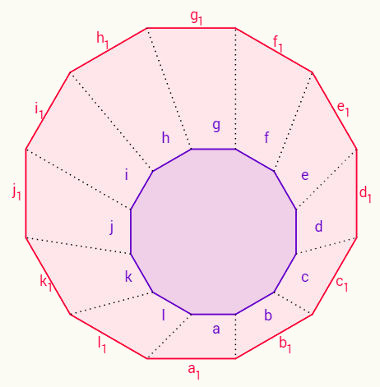
Observação: A soma dos ângulos externos de um polígono qualquer é igual a 360°.
Aproveite para conferir nossa videoaula sobre o assunto: