Na Geometria Plana, um elemento amplamente utilizado é o ângulo. Este se faz presente em inúmeras situações, ou seja, basta pensar em uma situação qualquer que é possível encontrar algum ângulo envolvido nela. Contudo, esse artigo foca apena os ângulos aplicados nas figuras geométricas e o estudo de suas propriedades.
Um polígono convexo possui dois tipos de ângulos: aqueles que são internos ao polígono e aqueles que são externos. O estudo das somas dos ângulos internos de um polígono pode ser visto no artigo “Soma dos ângulos internos de um polígono convexo”.
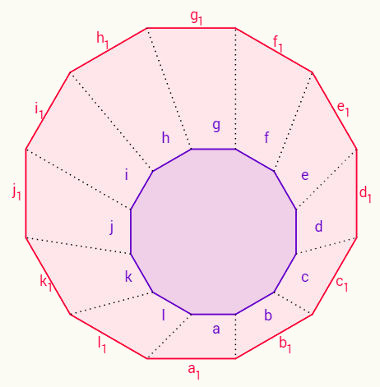
Por ora, faremos a demonstração da soma dos ângulos externos de qualquer polígono convexo. Portanto, partiremos de um caso concreto utilizando um pentágono e depois veremos um caso geral, com um polígono de n lados.

Exemplo de um pentágono
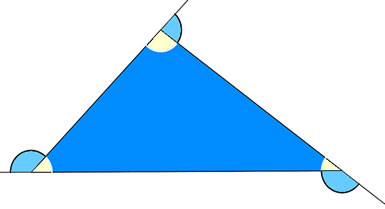
Veja que a soma do ângulo externo com o seu ângulo interno adjacente resulta em um ângulo de 180°, ou seja, são ângulos suplementares. Façamos a soma de todos os ângulos suplementares desse pentágono.
.jpg)
Vejamos se a soma dos ângulos externos será 360° para qualquer polígono convexo.
Sabemos que a soma dos ângulos internos é dada pela seguinte expressão:

Se somarmos os ângulos suplementares de um polígono convexo com n lados, teremos a seguinte expressão:

Ou seja, para qualquer que seja o polígono convexo, a soma dos seus ângulos externos será igual a 360°.