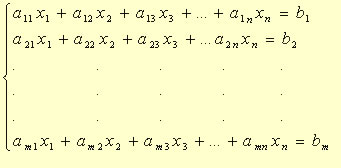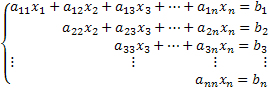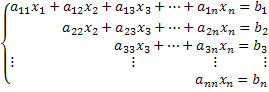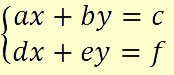Sistemas lineares

Sistema linear é um conjunto de equações lineares que estão relacionadas entre si, ou seja, possuem as mesmas soluções. Dizemos que uma equação é linear quando as suas variáveis possuem grau 1.

Existem vários métodos para resolver um sistema de equações lineares, como a regra de Cramer, em que apresentamos uma matriz associada ao sistema e encontramos os valores possíveis da incógnita por meio do determinante. Há também o escalonamento da matriz, no qual isolamos a variável e assim conseguimos encontrar o conjunto de soluções desse sistema.

Os sistemas lineares são utilizados para resolver equações que possuem mais de uma incógnita. Vale dizer também que há três tipos de sistemas lineares:

• sistema possível determinado;

• sistema possível indeterminado;

• sistema impossível.

Leia também: Classificação de sistemas lineares escalonados

Tópicos deste artigo

• 1 - Resumo sobre sistemas lineares
• 2 - Videoaula sobre sistemas lineares
• 3 - Equação linear
• 4 - O que são sistemas lineares?
• 5 - Matriz associada a um sistema linear
• 6 - Classificação de sistemas lineares
• 7 - Como resolver um sistema linear?
  • Regra de Cramer
  • Escalonamento
• 8 - Exercícios resolvidos sobre sistemas lineares

Resumo sobre sistemas lineares

• Um sistema linear é um conjunto de equações lineares.

• Para encontrar as soluções de um sistema linear, podemos utilizar, dentre outros métodos, a regra de Cramer ou o escalonamento.

• Existem três classificações possíveis para um sistema linear:

  • Sistema possível determinado (possui solução única);

  • Sistema possível indeterminado (possui infinitas soluções);

  • Sistema impossível (não possui soluções).

Videoaula sobre sistemas lineares

Equação linear

Para compreender o que são sistemas lineares, antes é importante rever o que é uma equação linear. Tem-se como equação linear qualquer equação que possui uma ou mais variáveis em que todas elas possuam grau 1. De forma geral, uma equação linear pode ser representada por:

a₁, a₂, a₃, … a_n → coeficientes das incógnitas

x₁, x₂, x₃, … x_n → incógnitas

b → termo independente

Exemplos:

a) x + 2y = 8

b) 3x – 2x + 3z = 0

c) x + y – z + 2w = 3

O que são sistemas lineares?

Conhecemos como sistema linear um conjunto de equações lineares que possuem as mesmas variáveis. A solução de um sistema linear é um conjunto de valores que é um resultado em comum de todas as equações envolvidas no sistema.

Exemplo:

Esse é um sistema linear 2x2, pois nele podemos identificar 2 equações e 2 incógnitas. Nesse sistema, podemos dizer que (5, 0) é a solução do sistema, pois satisfaz as duas equações ao mesmo tempo.

Dada a primeira equação 2x + 3y = 10, substituindo x = 5 e y = 0, temos que:

2 · 5 + 3 · 0 = 10 + 0 = 10

Na segunda equação, – x + y = – 5, substituindo também x = 5 e y = 0, temos que:

– 5 + 0 = – 5

Então, o par ordenado (5, 0) é a solução das duas equações, isto é, de todo o sistema de equações.

Leia também: Classificação de um sistema de equações

Matriz associada a um sistema linear

Podemos associar o sistema linear a uma matriz, prática comum dependendo do método de resolução que queremos adotar. Considere o sistema:

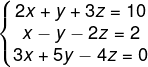
Nesse caso, podemos representar a matriz completa associada a esse sistema, expressa pelos coeficientes de cada uma das variáveis e do termo independente.

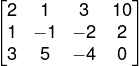
Há também a matriz incompleta, que é representada somente pelos coeficientes, excluindo a coluna dos termos independentes.

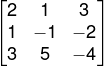
Classificação de sistemas lineares

Acontece que nem sempre um sistema possui uma única solução como o apresentado anteriormente. Existem, na verdade, três classificações possíveis para os sistemas lineares. Os sistemas classificam-se em: possível determinado, possível indeterminado e impossível.

• Sistema possível determinando: possui uma única solução.

• Sistema possível indeterminado: possui infinitas soluções.

• Sistema impossível: não possui soluções.

O sistema apresentado anteriormente foi um sistema possível determinado. Vejamos, agora, um exemplo de sistema possível indeterminado:

Quando as equações são múltiplas uma da outra, o sistema é possível indeterminado. Note que se multiplicarmos todos os termos da segunda equação por 2, encontraremos a primeira equação. Qualquer par ordenado que satisfaça a primeira equação satisfará a segunda também. Por exemplo:

• (10, 0) é solução das duas equações.

• (0, 5) é solução das duas equações.

• (6, 2) é solução das duas equações.

Como esse sistema é possível indeterminado, podemos listar infinitas soluções para ele.

Agora, vejamos um exemplo de sistema impossível:

Esse é um sistema impossível. Note que antes da igualdade, a segunda equação é o dobro da primeira. Porém, esse padrão não se repete no termo independente. Nesse caso, podemos dividir todos os termos da segunda equação por 2 e encontraremos o sistema:

É impossível que x + y seja igual a 10 e igual a 2 ao mesmo tempo. Logo, esse sistema de equações não possui solução, o que faz com que ele seja um sistema impossível.

Leia também: Método da substituição para solução de sistemas lineares

Como resolver um sistema linear?

Para resolver um sistema linear, existem vários métodos, porém faremos a apresentação de apenas dois deles: a regra de Cramer e o escalonamento.

• Regra de Cramer

Para resolver um sistema 3x3 utilizando a regra de Cramer, é necessário calcular o determinante da matriz incompleta e suas variações. Temos que:

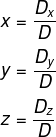
• D → determinante da matriz incompleta;

• D_x → determinante da matriz incompleta do sistema, substituindo a coluna de x pela coluna dos termos independentes;

• D_y → determinante da matriz incompleta do sistema, substituindo a coluna de y pela coluna dos termos independentes;

• D_z → determinante da matriz incompleta do sistema, substituindo a coluna de z pela coluna dos termos independentes.

Exemplo:

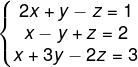
• 1º passo: Calcularemos o determinante da matriz incompleta.

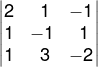
D = 2 ⋅ (−1) ⋅ (−2) + 1 ⋅ 1 ⋅ 1 + (−1) ⋅ 1 ⋅ 3 − 1 ⋅ (−1) ⋅ (−1) − 3 ⋅ 1 ⋅ 2 − (−2) ⋅ 1 ⋅ 1 = − 3

• 2º passo: Em seguida, substituiremos a primeira coluna pelos termos independentes do sistema e novamente calcularemos o determinante (no caso, D_x).

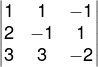
D_x = 1 ⋅ (−1) ⋅ (−2) + 1 ⋅ 1 ⋅ 2 + (−1) ⋅ 2 ⋅ 3 − 2 ⋅ (−1) ⋅ (−1) − 3 ⋅ 1 ⋅ 1 − (−2) ⋅ 2 ⋅ 1 = −3

• 3º passo: Na matriz incompleta, substituiremos a segunda coluna pelos termos independentes e calcularemos o determinante D_y.

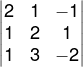
D_y = 2 ⋅ 2 ⋅ (−2) + 1 ⋅ 1 ⋅ 1 + (−1) ⋅ 1 ⋅ 3 − 1 ⋅ 2 ⋅ (−1) − 3 ⋅ 1 ⋅ 2 − (−2) ⋅ 1 ⋅ 1 = −12

• 4º passo: Substituiremos, na matriz incompleta, a terceira coluna pelos termos independentes e calcularemos o determinante D_z.

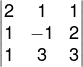
D_z = 2 ⋅ (−1) ⋅ 3 + 1 ⋅ 2 ⋅ 1 + 1 ⋅ 1 ⋅ 3 − 1 ⋅ (−1) ⋅ 1 − 3 ⋅ 2 ⋅ 2 − 3 ⋅ 1 ⋅ 1 = −15

Agora é possível encontrar os valores de x, y e z:

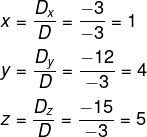
Descobrimos, assim, que o conjunto de soluções desse sistema é (1, 4, 5).

• Escalonamento

O escalonamento é outro método comum utilizado para resolver sistemas lineares. Escalonar uma matriz consiste em realizar operações entre suas linhas de modo que os coeficientes do sistema resultem em zero.

Exemplo:

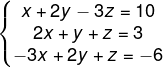
• 1º passo: Listaremos a matriz completa associada ao sistema:

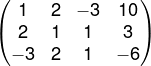
• 2º passo: Faremos operações entre as linhas para que na primeira coluna os termos a₂₁ e a₃₁ sejam igual a 0. Para isso, considere que:

  • L₁ = linha 1

  • L₂ = linha 2

  • L₃ = linha 3

Então, substituiremos a linha 2 por: L₂ = –2L₁ + L₂

a₂₁ = –2 · 1 + 2 = 0

a₂₂ = –2 · 2 + 1 = –3

a₂₃ = –2 · (–3) + 1 = 7

a₂₄ = –2 · 10 + 3 = –17

Além da linha 2, vamos substituir a linha 3 por: L₃ = 3L₁ + L₃

a₃₁ = 3 · 1 – 3 = 0

a₃₂ = 3 · 2 + 2 = 8

a₃₃ = 3 · (–3) + 1 = – 8

a₃₄ = 3 · 10 – 6 = 24

Analisando os termos da linha três, percebe-se que podemos simplificá-la, dividindo por 8. Então, temos que:

a₃₁ = 0 : 8 = 0

a₃₂ = 8 : 8 = 1

a₃₃ = – 8 : 8 = 1

a₃₄ = 24 : 8 = 3

Substituindo os valores que encontramos na matriz, teremos o seguinte:

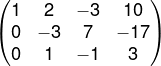
Assim, vamos zerar os coeficientes de y na terceira linha a fim de obtermos uma matriz triangular. Para isso, substituiremos L₃ por L₃ → L₂ + 3L₃.

a₃₁ = 0 + 3 · 0 = 0

a₃₂ = –3 + 3 · 1 = 0

a₃₃ = 7 + 3 · (–1) = 4

a₃₄ = –17 + 3 · 3 = –8

A nova matriz escalonada será:

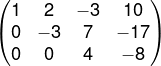
Agora podemos reescrever essa matriz como um sistema:

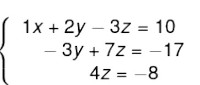
Desse modo, pela terceira equação, temos que:

4z = –8

z = – 8 : 4

z = –2

Substituindo z por – 2 na segunda linha, temos que:

–3y + 7 (–2) = –17

–3y – 14 = –17

–3y = –17 + 14

–3y = –3

y = –3 : (–3)

y = 1

Por fim, substituindo y = 1 e z = – 2 na linha 1, temos que:

x + 2 · 1 – 3 (–2) = 10

x + 2 + 6 = 10

x – 8 = 10

x = 10 – 8

x = 2

Concluímos, então, que o conjunto de soluções dessa equação é (2, 1, –2)

Leia também: Método da adição para solução de sistemas lineares

Exercícios resolvidos sobre sistemas lineares

Questão 1

(Consulpam) O valor de x no sistema linear a seguir é:

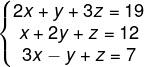
A) 1

B) 2

C) 3

D) 4

Resolução:

Alternativa B

Para encontrar o valor de x pela regra de Cramer, calcularemos o valor do determinante D da matriz incompleta e também do determinante D_x.

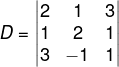
D = 2 ⋅ 2 ⋅ 1 + 1 ⋅ 1 ⋅ 3 + 3 ⋅ 1 ⋅ (−1) − 3 ⋅ 2 ⋅ 3 − (−1) ⋅ 1 ⋅ 2 − 1 ⋅ 1 ⋅ 1 = −13

Agora, substituindo a primeira coluna pela coluna das variáveis independentes, temos:

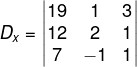
D_x = 19 ⋅ 2 ⋅ 1 + 1 ⋅ 1 ⋅ 7 + 3 ⋅ 12 ⋅ (−1) − 7 ⋅ 2 ⋅ 3 − (−1) ⋅ 1 ⋅ 19 − 1 ⋅ 12 ⋅ 1 = −26

Sabemos que x é a divisão entre D_x e D:

x = D_x : D

x = (–26) : (–13)

x = 2

Questão 2

(Idib) É correto afirmar que a regra de Cramer é um método utilizado para:

A) desenvolver operação com conjuntos.

B) determinar o volume de um cone utilizando uma esfera.

C) determinar o resultado de uma progressão geométrica infinita.

D) solucionar sistemas lineares.

Resolução:

Alternativa D

Como vimos, a regra de Cramer é um método utilizado para encontrar as soluções de sistemas lineares.