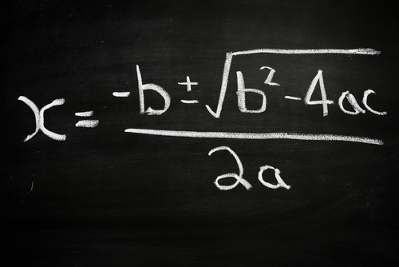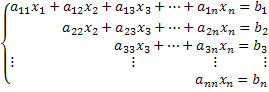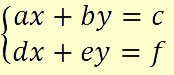Existem diversos métodos de resolução para um sistema de equações. Quando esse sistema possui apenas duas equações e é classificado como possível e determinado, pode-se resolvê-lo usando o método da adição.
Esse método consiste em somar as equações de um sistema termo a termo. Ele é indicado para os casos em que uma das incógnitas aparece na primeira equação com valor positivo e, na segunda, com valor negativo, como no exemplo a seguir:
Esse método também é indicado para qualquer caso em que um dos termos de uma das equações é múltiplo de um dos termos da outra, como mostra o exemplo seguinte:
Nos demais casos, o método da adição pode ser usado, mas envolve mais passos ou mais multiplicações com números decimais, o que possivelmente tornará a solução do problema mais difícil do que por outro método.
Para facilitar o aprendizado, o método da adição será discutido em passos a serem seguidos. Para isso, usaremos como exemplo o seguinte sistema:
Primeiro passo: organizar os termos do sistema
Como o método envolve a soma de termos, esses termos devem ser semelhantes, ou seja, devem possuir a mesma incógnita. Para facilitar esse procedimento, é melhor posicionar os termos semelhantes um logo abaixo do outro no sistema. Assim, teremos no exemplo:
Segundo passo: multiplicar uma das equações por uma constante apropriada
Quando um dos termos de uma equação for o oposto aditivo de um dos termos da outra equação, não será preciso utilizar este passo. No caso do exemplo, note que os termos – 2y e – 6y são múltiplos. Para que se tornem opostos aditivos, basta multiplicar – 2y por – 3. O resultado dessa multiplicação é 6y, que é o oposto aditivo de – 6y da segunda equação.
Para fazer essa multiplicação e não alterar o resultado do sistema, basta multiplicar todos os termos da primeira equação por esse mesmo fator – 3. Observe:
Terceiro passo: somar as equações
A partir desse resultado, faça a adição algébrica das duas equações termo a termo. O resultado disso será uma equação do primeiro grau. Resolvendo-a, encontraremos o resultado da primeira incógnita. Observe:
Repare que o objetivo desse método é zerar uma das incógnitas após a soma das equações. Se isso não acontecer, todo o processo deve ser revisto, pois algum erro foi cometido.
Quarto passo: encontrar o valor numérico da segunda incógnita
Para fazer esse último passo, basta substituir o valor numérico da incógnita encontrada em uma das duas equações iniciais. Faremos isso com a primeira equação:
Aproveite para conferir nossa videoaula sobre o assunto: