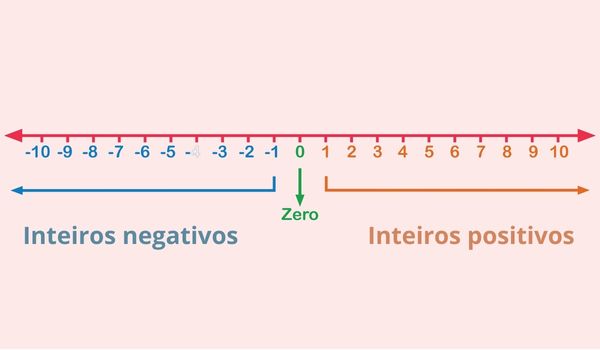
É no conjunto dos inteiros que nos deparamos com os números positivos e negativos. Esse conjunto é representada pela letra (Z). Veja um exemplo:
Z= {…- 5, - 4, - 3, - 2, - 1, 0, + 1, + 2, + 3, + 4, + 5 ...}
O conceito que envolve oposto ou simétrico está diretamente relacionado com o conjunto dos números inteiros. Isso acontece porque todo número, seja ele positivo, seja negativo, possui um oposto ou simétrico. Sendo assim:
-
O oposto ou simétrico de + 1 é -1.
-
O oposto ou simétrico de – 1 é + 1.
-
O oposto ou simétrico de + 5 é – 5.
-
O oposto ou simétrico de – 5 é + 5.
-
O oposto ou simétrico de + 2000 é – 2000.
-
O oposto ou simétrico de – 2000 é + 2000.
-
O oposto ou simétrico de + 5000 é – 5000.
-
O oposto ou simétrico de – 5000 é + 5000.
OPOSTO OU SIMÉTRICO DE UM NÚMERO NA RETA NUMÉRICA
Na reta numérica dos números inteiros, chamamos o zero de origem. Os números que são opostos ou simétricos sempre terão a mesma distância em relação à origem.

-
+ 4 é simétrico ou oposto a – 4 e vice-versa.
Distância de + 4 a 0 → +4 – 0 = + 4
Distância de – 4 a 0 → 0 – (– 4) = + 4
Conclusão: + 4 e – 4 possuem a mesma distância em relação à origem. -
+ 3 é simétrico ou oposto a – 3 e vice-versa.
Distância de + 3 a 0 → + 3 – 0 = + 3
Distância de – 3 a 0 → 0 – ( – 3) = + 3
Conclusão: + 3 e – 3 possuem a mesma distância em relação à origem. -
+ 2 é simétrico ou oposto a – 2 e vice-versa.
Distância de + 2 a 0 → + 2 – 0 = + 2
Distância de – 2 a 0 → 0 – (– 2) = + 2
Conclusão: + 2 e – 2 possuem a mesma distância em relação à origem. -
+ 1 é simétrico ou oposto a – 1 e vice-versa.
Distância de + 1 a 0 → + 1 – 0 = + 1
Distância de – 1 a 0 → 0 – (– 1) = + 1
Conclusão: + 1 e – 1 possuem a mesma distância em relação à origem.