Nos primeiros estudos da trigonometria, aprendemos os elementos que compõem um triângulo retângulo. Entretanto, aprendemos de forma simples, sem ter grande compreensão do que de fato ocorre nessas relações trigonométricas tão importantes.
Façamos uma revisão quanto aos elementos de um triângulo retângulo.
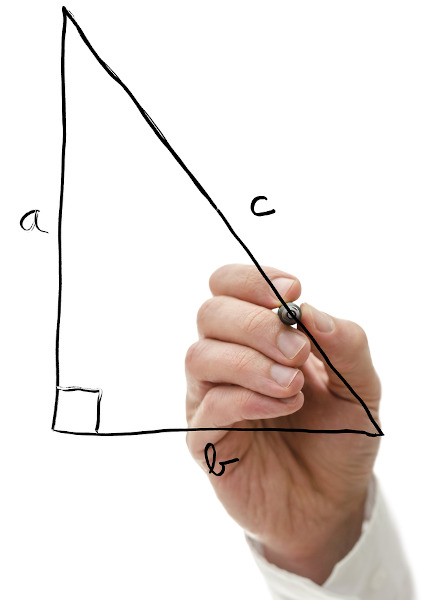
Veja que:
• a consiste na medida da hipotenusa (lado oposto ao ângulo reto);
• b e c são as medidas dos catetos;
• Os ângulos dos vértices C e B são ângulos agudos;
• O segmento AC é o cateto oposto ao ângulo do vértice B, que por sua vez é o cateto adjacente ao ângulo do vértice C;
• O segmento AB é o cateto oposto ao ângulo do vértice C, que por sua vez é adjacente ao ângulo do vértice B.
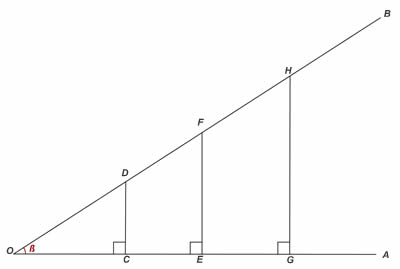
Relembrando esses elementos, façamos uma construção de triângulos semelhantes para analisarmos as proporcionalidades dessa semelhança.
Você consegue identificar três triângulos semelhantes? Veja que na imagem acima temos três triângulos retângulos: ΔDOC, ΔFOE, ΔHOG.
Em um dos casos de semelhança de triângulos têm-se a necessidade de termos dois ângulos congruentes, isso nos dá a garantia de que os triângulos são semelhantes.
Portanto, note que nos três triângulos podemos aplicar esse caso de semelhança, pois o ângulo β é comum a todos os triângulos e todos eles possuem um ângulo reto. Sendo assim, vejamos algumas razões de proporcionalidade que teremos em razão de serem triângulos semelhantes.
.png){kind=small}
Como estes triângulos são semelhantes, podemos afirmar que estas razões são iguais entre si e resultam um valor em comum, ou seja:
.png){kind=small}
Contudo, temos que os segmentos DC, FE, HG constituem os catetos opostos ao ângulo β. Os segmentos OD, OF, OH são as hipotenusas dos triângulos ΔDOC, ΔFOE, ΔHOG, respectivamente.
Sabemos que:
.png){kind=small}
De acordo com o que foi visto anteriormente, as razões da medida do cateto oposto pela medida da hipotenusa correspondem a uma proporção equivalente, sendo assim, podemos afirmar que:
.png){kind=small}
Portanto, podemos afirmar que esta relação não depende do tamanho que é o triângulo e sim do ângulo β, esta relação é denominada de seno de β.
Diante disso, existe a necessidade de o triângulo ser retângulo para que se possa utilizar a relação do seno, pois como vimos, só foi possível determinar as proporcionalidades dos triângulos por serem triângulos retângulos.
Videoaula relacionada:
