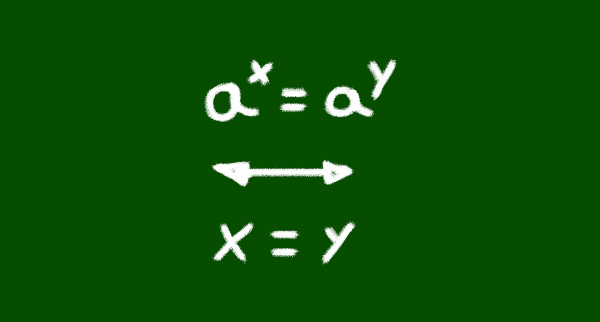As equações exponenciais são caracterizadas pela presença da incógnita no expoente de uma ou mais potências de bases positivas e diferentes de 1. Exemplos:
2x–2 = 16
2x+1 + 2x = 6
3x+2 – 3x = 27
3x+2 – 3x = 216
2x–4 – 2x–3 + 2x–2 = 24
Elas são muito utilizadas na resolução de problemas envolvendo juros compostos, crescimento populacional, situações que envolvam grandes variações durante um pequeno intervalo de tempo, decaimento radioativo, progressões geométricas, crescimento de determinadas plantas entre outras situações.
O método resolutivo de uma equação exponencial consiste em reduzir as bases ao mesmo valor, igualando os expoentes. Observe:
ax1 = ax2 ↔ x1 = x2 (a > 0 e a ≠ 1)
Exemplo 1
2x = 32
32 = 25
2x= 25
x = 5
Exemplo 2
4x = 64
64 = 43
4x = 43
x = 3
Exemplo 3
816 + x = 9 –2x
34*(6+x) = 32*(–2x)
324 + 4x = 3 –4x
24 + 4x = –4x
4x+4x = –24
8x = –24
x = –24/8
x = –3
Exemplo 4
5x + 5x+1 = 30
5x + 5x * 5 = 30
Substituindo 5x por y.
y + y*5 = 30
y + 5y = 30
6y = 30
y = 30/6
y = 5
Retornando termos:
5x = y
5x = 5
x = 1
Exemplo 5
2x * 23 + 2x = 9
Substituindo 2x = y
y * 8 + y = 9
8y + y = 9
9y = 9
y = 1
Retornando:
2x = 1
2x = 20
x = 0
Exemplo 6
3x+2 – 3x = 216
3x * 32 – 3x = 216
Substituindo 3x = y
y * 9 – y = 216
9y – y = 216
8y = 216
y = 216/8
y = 27
Retornando
3x = 27
3x = 3³
x = 3