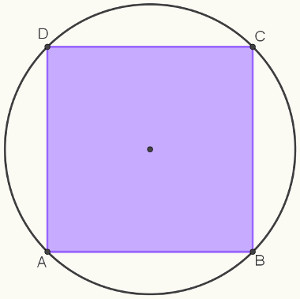
Dizemos que um quadrado é inscrito em uma circunferência quando todos os seus vértices pertencem a ela. Como o quadrado é um polígono regular – que possui todos os lados com a mesma medida e ângulos internos congruentes –, existem relações que podem ser usadas para calcular a medida de seu lado e de seu apótema a partir apenas do raio da circunferência. Para isso, vale lembrar de algumas definições básicas do polígono regular inscrito:
Elementos básicos do polígono regular inscrito
1 – Centro: O centro de um polígono regular inscrito tem a mesma localização que o centro da circunferência que o circunscreve.
2 – Raio: O raio de um polígono regular inscrito é a distância entre seu centro e a borda da circunferência. Como se trata de um polígono, essa distância só pode ser obtida entre o centro do polígono e um de seus vértices.
3 – Apótema: É a distância entre o centro de um polígono regular e o ponto médio de um de seus lados. No caso do quadrado inscrito, o apótema também forma um ângulo reto com o lado com o qual faz contato.
A imagem a seguir mostra um exemplo dos elementos citados:
Relações métricas no quadrado inscrito
1 – O lado do quadrado inscrito é igual ao raio multiplicado pela raiz de 2. Em outras palavras:
l = r√2
2 – O apótema do quadrado inscrito é igual à metade da medida do raio, multiplicado pela raiz de 2. Em outras palavras:
a = r√2
2
Demonstração das relações métricas no quadrado inscrito
Para demonstrar essas relações, será necessário observar primeiro as seguintes informações:
1 – Como o apótema divide o lado do quadrado em dois segmentos congruentes, podemos dizer que a medida de cada um deles é igual a l/2.
2 – Como se trata de um polígono regular, o apótema e o lado com o qual ele se encontra são perpendiculares.
3 – Como se trata de um polígono regular, o apótema também é bissetriz do ângulo central que ele corta.
Observe que cada ângulo central, definido por dois raios consecutivos em um quadrado inscrito, sempre é reto. Isso acontece porque todos os ângulos têm de ser iguais, já que o quadrado é um polígono regular. Como são quatro ângulos centrais, então: 360/4 = 90°. O apótema é bissetriz desse ângulo, portanto, divide-o em outros dois ângulos de 45°.
Colocando todas essas informações em uma figura de um quadrado inscrito, temos:
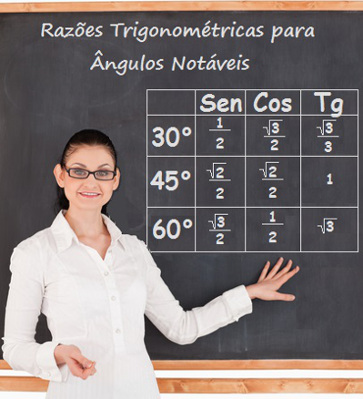
Ao lado, separamos o triângulo OPB formado por um dos raios e um dos apótemas. Nesse triângulo, podemos calcular o seno e o cosseno de 45°. Observe:
Sen45° = l/2
r
√2 = l
2 2
r
√2 = l
2 2r
r√2 = l
l = r√2
Cos45° = a
r
√2 = a
2 r
r√2 = a
2
a = r√2
2
Exemplo:
Calcule a medida do lado e do apótema de um quadrado inscrito em uma circunferência de raio igual a 100 cm.
Solução: Para obter essas medidas, basta substituir o valor do raio nas fórmulas do apótema e do lado do quadrado inscrito na circunferência:
l = r√2
l = 100√2
a = r√2
2
a = 100√2
2
a = 50√2