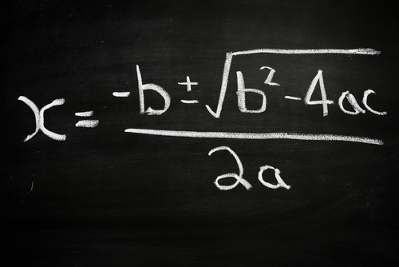Albert Girard aprofundou, aproximadamente no ano de 1629, os estudos sobre as raízes de equações do 2º grau criando relações entre os coeficientes a, b e c. Essas relações determinam a soma e o produto das raízes de uma equação do 2º grau. Observe a demonstração:
Uma equação do 2º grau possui a seguinte lei de formação: ax² + bx + c = 0. As raízes dessa equação são dadas por x1 e x2. Veja:

Determinando a soma das raízes:
![]()
Determinando o produto das raízes

As relações são utilizadas antecipando o cálculo das raízes. Dessa forma, não precisamos determinar o valor do discriminante ao utilizar a fórmula de Bháskara. As expressões criadas por Girard oferecem a soma e o produto através somente dos valores dos coeficientes numéricos da equação do 2º grau.
Vamos determinar a soma e o produto das raízes envolvendo as seguintes equações do 2º grau.
Exemplo 1

Exemplo 2