O matemático suíço Leonhard Euler (1707-1783) encontrou uma relação entre os vértices, arestas e faces de qualquer poliedro convexo. Vamos então relembrar algumas definições:
-
Poliedro: são sólidos formados pelo encontro de planos;
-
Poliedro convexo: um poliedro é dito convexo se suas faces não formam nenhuma “cavidade”. Exemplo de um poliedro não convexo:

Esse poliedro apresenta uma “concavidade” que o caracteriza como um poliedro não convexo
-
Vértice: é formado pelo encontro de duas retas (arestas);
-
Arestas: é a reta formada pelo encontro de duas faces;
-
Face: é cada região plana do poliedro, delimitada por arestas.
No paralelepípedo a seguir, vamos identificar o número de faces, arestas e vértices:

O paralelogramo possui 6 faces, 8 vértices e 12 arestas
No paralelogramo, há 6 “lados” retangulares que representam as faces, assim como a face rosa já contabilizada. Os 12 segmentos de reta pretos representam as arestas, e os 8 pontos vermelhos representam os vértices.
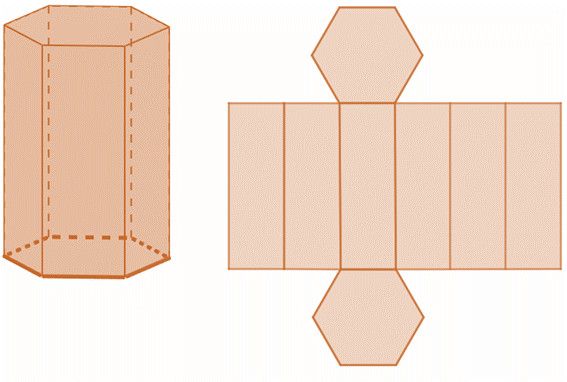
Vejamos o que acontece com um prisma de base pentagonal:

O prisma de base pentagonal possui 7 faces, 10 vértices e 15 arestas
O prisma de base pentagonal possui 7 faces, 10 vértices e 15 arestas. Se você observar bem, nesses dois exemplos há uma relação entre o número de vértices e faces e o número de arestas. Vejamos:
Paralelogramo → 8 V e 6 F ←→ 12 A
Prisma de Base Pentagonal → 10 V e 7 F ←→ 15 A
Some os números de vértices e faces e compare-os com o número de arestas. Você verá que a soma será duas unidades maior que o número de arestas. Se generalizarmos essa ideia, teremos:
V + F = A + 2
Essa equação representa a Relação de Euler. Verifiquemos se ela é válida para outros poliedros:
Seja um poliedro com 4 vértices e 4 faces, qual sua quantidade de arestas?

A pirâmide de base triangular possui 4 faces, 4 vértices e 6 arestas
-
V + F = A + 2
-
4 + 4 = A + 2
-
A + 2 = 8
-
A = 8 – 2
A = 6 arestas
Tome um poliedro com 6 vértices e 9 arestas, qual seu número de faces?

O prisma de base triangular possui 5 faces, 6 vértices e 9 arestas
V + F = A + 2
6 + F = 9 + 2
6 + F = 11
F = 11 – 6
F = 5 faces
*Créditos da imagem: Shutterstock e William Perugini
Aproveite para conferir nossas videoaulas sobre o assunto: