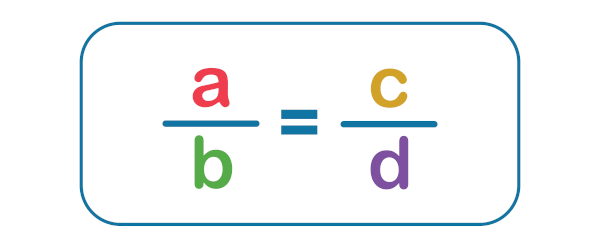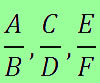Razão e proporção

Razão e proporção são dois conceitos muito presentes em diversas atividades cotidianas e áreas do conhecimento, também são cobrados com frequência na prova do Enem.

Razão é o quociente (resultado de uma divisão) entre dois números reais; proporção é uma igualdade entre razões.

Leia também: Três erros comuns na regra de três

Tópicos deste artigo

• 1 - Resumo sobre razão e proporção
• 2 - Videoaula sobre razão e proporção
• 3 - O que é razão?
• 4 - O que é proporção?
  • ? Propriedades da proporção
• 5 - Como calcular a razão e a proporção?
• 6 - Exercícios resolvidos sobre razão e proporção

Resumo sobre razão e proporção

• Razão é o quociente entre dois números reais.

• Uma razão pode ocorrer entre elementos de uma mesma grandeza ou entre elementos de grandezas diferentes.

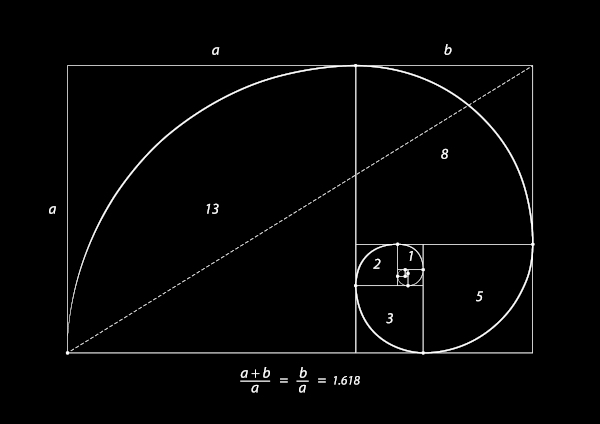
• A razão áurea (ou número de ouro) é uma medida associada ao equilíbrio e à harmonia.

• Proporção é uma igualdade entre razões.

• A regra de três é uma propriedade da proporção.

• Uma proporção pode relacionar grandezas de maneira direta ou indireta.

Videoaula sobre razão e proporção

O que é razão?

Razão é o resultado da divisão entre dois números reais. Se a e b são números reais, então \(\frac{a}b\), com \(b≠0\), é a razão entre a e b.

Exemplo:

Qual a razão entre 1 e 2?

A razão entre 1 e 2 é \(\frac{1}2\). Além da representação fracionária, a razão pode ser indicada pela representação decimal (0,5) ou percentual (50%).

É importante destacar que a razão pode indicar uma divisão entre grandezas de mesma espécie (e, portanto, é apenas um número, sem unidade) ou entre grandezas de espécies diferentes. Veja alguns casos:

• O número π é um exemplo de razão entre grandezas de mesma espécie, pois é a razão entre o comprimento de uma circunferência e seu diâmetro.

• Uma medida de probabilidade é um exemplo de razão entre grandezas de mesma espécie, pois indica a razão entre casos favoráveis e casos possíveis de um espaço amostral.

• A velocidade média de um corpo é um exemplo de razão entre grandezas de espécies diferentes, pois corresponde à razão entre o deslocamento (medido em centímetros, metros, quilômetros etc.) e o tempo (medido em segundos, minutos, horas etc.). Algumas unidades de medida de velocidade média são o m/s (metros por segundo) e o km/h (quilômetros por hora).

• A densidade demográfica é um exemplo de razão entre grandezas de espécies diferentes, pois indica a razão entre o número de habitantes de uma região e a área que esses habitantes ocupam. A unidade de medida mais utilizada para densidade demográfica é hab/km² (habitantes por quilômetro quadrado).

Perceba que, nas razões entre grandezas de espécies diferentes, as próprias unidades de medida indicam uma razão pelo sinal de /.

Uma das aplicações mais importantes da ideia de razão é a escala cartográfica.

O que é proporção?

Proporção é uma igualdade entre razões. Considere que uma razão \(\frac{a}b\) resulta em certo valor x e que outra razão \(\frac{c}d\) também resulta no mesmo valor x. Portanto, podemos escrever:

\(\frac{a}b=\frac{c}d\)

Dizemos que a sobre b é proporcional a c sobre d ou que a está para b assim como c está para d.

A proporção é a estrutura matemática que relaciona grandezas direta e inversamente proporcionais.

➝ Propriedades da proporção

As propriedades mais importantes da proporção são:

1. O produto dos meios é igual ao produto dos extremos.

Também conhecida como multiplicação cruzada ou regra de três, essa propriedade estabelece que:

\(\frac{a}b=\frac{c}d→a\cdot d=c\cdot b\)

Perceba que podemos utilizar essa propriedade para encontrar um termo desconhecido de uma proporção.

2. A soma (ou diferença) dos numeradores e denominadores de razões proporcionais é proporcional a cada uma.

Em notação matemática, isso significa que:

\(\frac{a}b=\frac{c}d=\frac{a+c}{b+d}\)

e

\(\frac{a}b=\frac{c}d=\frac{a-c}{b-d}\)

Leia também: Como proporção aparece no Enem?

Como calcular a razão e a proporção?

Em muitos casos, os conceitos de razão e proporção estão implícitos na resolução de um problema. Vejamos alguns exemplos.

Exemplo 1: João precisa comprar um caderno novo para o início das aulas. Ele está na dúvida entre um caderno que custa R$ 9 e outro que custa R$ 13,50. Qual a relação entre o caderno mais caro e o mais barato?

a) \(\frac{7}3\)

b) \(\frac{5}2\)

c) \(\frac{3}2\)

d) \(\frac{1}2\)

e) \(\frac{1}3\)

Perceba que a relação entre o caderno mais caro e o mais barato é expressa como uma razão. Assim,

\(\frac{R$\ 13,50}{R$\ 9}=\frac{3}2\)

Alternativa C

Exemplo 2: Pedro está seguindo uma receita que encontrou na internet, mas precisará adaptar as medidas, pois está cozinhando para toda a família. Sabendo que 3 xícaras de farinha produzem 20 porções, quantas xícaras ele deve utilizar para conseguir 30 porções?

Perceba que a relação entre a quantidade de xícaras e as porções produzidas é proporcional: quanto mais xícaras, mais porções, e, por exemplo, se Pedro dobrar a quantidade de xícaras, dobrará a quantidade de porções recebidas (mas, neste caso, teria 40 porções).

Para resolver esse problema, podemos montar a proporção relacionada:

\(\frac{3\ xícaras}{20\ porções}=\frac{n\ xícaras}{30\ porções}\)

Utilizando a propriedade 1, concluímos que n = 4,5, ou seja, Pedro precisará de 4 xícaras e meia.

Exercícios resolvidos sobre razão e proporção

Questão 1

(Enem 2021) Um parque temático brasileiro construiu uma réplica em miniatura do castelo de Liechtenstein. O castelo original, representado na imagem, está situado na Alemanha e foi reconstruído entre os anos de 1840 e 1842, após duas destruições causadas por guerras.

O castelo possui uma ponte de 38,4 m de comprimento e 1,68 m de largura. O artesão que trabalhou para o parque produziu a réplica do castelo, em escala. Nessa obra, as medidas do comprimento e da largura da ponte eram, respectivamente, 160 cm e 7 cm.

A escala utilizada para fazer a réplica é

a) 1 : 576

b) 1 : 240

c) 1 : 24

d) 1 : 4,2

e) 1 : 2,4

Resolução: alternativa C

A escala é a razão entre a medida utilizada pelo artesão e a medida real. Escolhendo comparar o comprimento, por exemplo, temos que:

\(\frac{160\ cm}{3840\ cm}=\frac{1}{24}\)

Questão 2

(Enem 2020) Uma empresa de ônibus utiliza um sistema de vendas de passagens que fornece a imagem de todos os assentos do ônibus, diferenciando os assentos já vendidos, por uma cor mais escura, dos assentos ainda disponíveis. A empresa monitora, permanentemente, o número de assentos já vendidos e compara-o com o número total de assentos do ônibus para avaliar a necessidade de alocação de veículos extras.

Na imagem tem-se a informação dos assentos já vendidos e dos assentos ainda disponíveis em um determinado instante.

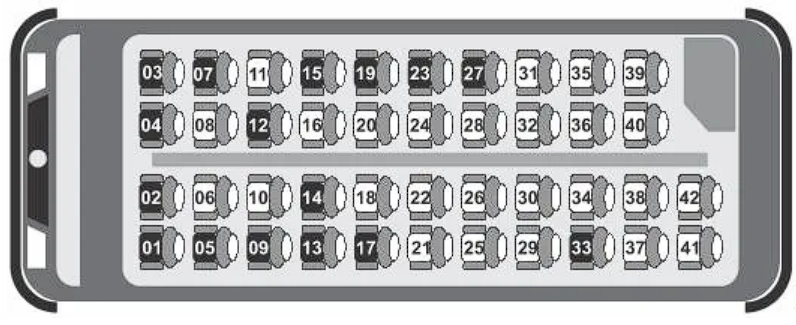
A razão entre o número de assentos já vendidos e o total de assentos desse ônibus, no instante considerado na imagem, é:

a) \(\frac{16}{42}\)

b) \(\frac{16}{24}\)

c) \(\frac{26}{42}\)

d) \(\frac{42}{26}\)

e) \(\frac{42}{16}\)

Resolução: alternativa A

De acordo com a imagem, 16 assentos já foram vendidos. Ainda, o total de assentos desse ônibus é 42. Portanto, a razão entre o número de assentos já vendidos e o total de assentos é \(\frac{16}{42}\).