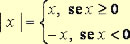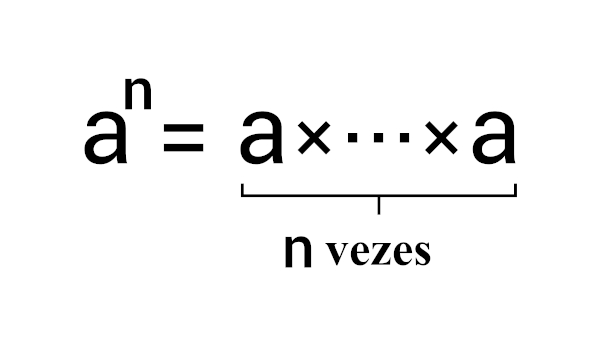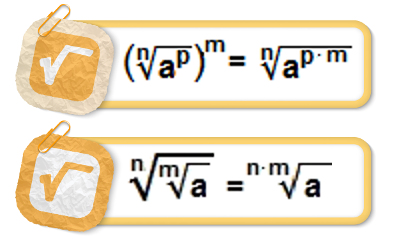Raiz quadrada é um caso particular da operação de radiciação. Dizemos que a raiz quadrada de um número x é igual a y se y ao quadrado é igual a x. Em notação matemática, escrevemos \(\sqrt x = y\) se \(y^2=x\) .
Leia também: Propriedades da radiciação — fique por dentro para facilitar os cálculos com raiz
Tópicos deste artigo
- 1 - Resumo sobre raiz quadrada
- 2 - Videoaula sobre raiz quadrada
- 3 - O que é raiz quadrada?
- 4 - Lista de raízes quadradas
- 5 - Radiciação e raiz quadrada
- 6 - Como calcular uma raiz quadrada?
- 7 - Tipos de raiz quadrada
- 8 - Quais são as propriedades da raiz quadrada?
- 9 - Exercícios resolvidos sobre raiz quadrada
Resumo sobre raiz quadrada
-
A raiz quadrada é um caso específico de radiciação.
-
O índice de uma raiz quadrada é 2 e pode ser expresso ou ficar subentendido.
-
Calcular a raiz quadrada de um número x é buscar um número y tal que \(y^2=x\).
-
Se o resultado de uma raiz quadrada é um número racional, dizemos que a raiz é exata; do contrário, é não exata.
Videoaula sobre raiz quadrada
O que é raiz quadrada?
A raiz quadrada é um caso particular de radiciação. Dizer que a raiz quadrada de x é igual a y significa dizer que \(y^2\) é igual a x.
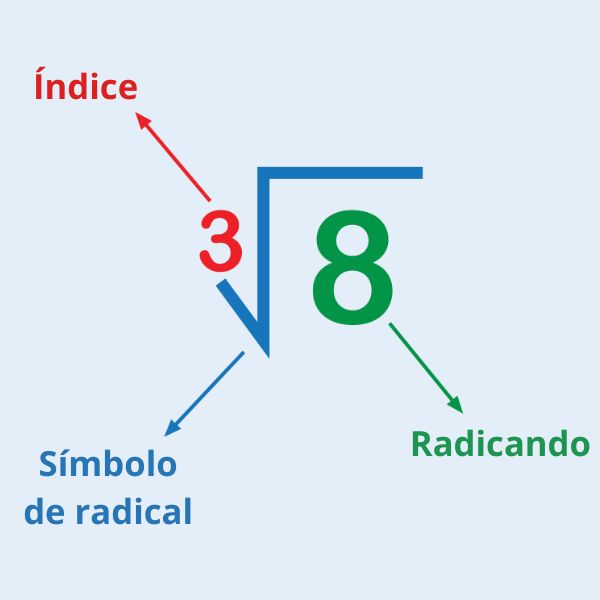
Para expressar a raiz quadrada de x, utilizamos os símbolos \(\sqrt x\) ou \(\sqrt[2]{x}\). Nessa representação, x é o radicando, e 2 é o índice.
Formalmente,
\(\sqrt x=y\) se \( y^2=x\), com x e y reais positivos
Assim, podemos compreender a raiz quadrada como a operação inversa da potenciação com expoente 2.
Lista de raízes quadradas
Vejamos algumas das raízes quadrada mais comuns:
\(\sqrt0=0\)
\(\sqrt1=1\)
\(\sqrt2= 1,414213562…\)
\(\sqrt3=1,7320508…\)
\(\sqrt4=2\)
\(\sqrt5=2,2360679…\)
\(\sqrt8=2,828427125…\)
\(\sqrt9=3\)
\(\sqrt{16}=4\)
\(\sqrt{25}=5\)
\(\sqrt{36}=6\)
\(\sqrt{49}=7\)
\(\sqrt{64}=8\)
\(\sqrt{81}=9\)
\(\sqrt{100}=10\)
\(\sqrt{121}=11\)
\(\sqrt{144}=12\)
\(\sqrt{169}=13\)
\(\sqrt{196}=14\)
\(\sqrt{225}=15\)
Radiciação e raiz quadrada
A radiciação é operação inversa da potenciação. Se x e y são reais positivos, a raiz enésima de x é definida da seguinte maneira:
\(\sqrt[n]{x}=y\) se \(y^n=x\)
Observe que a raiz quadrada é o caso especial em que n 2.
Observação: é possível expandir a definição de radiciação para valores de x negativos. Como consequência, os valores de y serão números complexos. Para mais detalhes sobre esses números, clique aqui.
Como calcular uma raiz quadrada?
Para calcular (ou extrair) a raiz quadrada de um número x, devemos buscar um número y tal que \( y^2=x\).
Encontrar y pode ser uma tarefa simples ou difícil, dependendo de qual é o valor de x. O uso da calculadora e a fatoração do radicando em números primos são estratégias de cálculo da raiz quadrada.
Exemplos:
\(\sqrt9=3\), pois \(3^2=9\)
\(\sqrt{0,64}=0,8\), pois \(0,8^2=0,64\)
Tipos de raiz quadrada
Se uma raiz quadrada é um número racional, então é uma raiz exata.
\(\sqrt4\) é uma raiz exata, pois \(\sqrt4=2\), e 2 é um número racional.
\(\sqrt{2,25}\) é uma raiz exata, pois \(\sqrt{2,25=1,5}\), e 1,5 é um número racional.
Se uma raiz quadrada é um número irracional, então é uma raiz não exata. Lembre-se de que os números irracionais são aqueles cuja representação decimal é infinita e não periódica.
\(\sqrt2\) é uma raiz não exata, pois \(\sqrt{2}=1,4142135… \) , que é um número irracional.
\(\sqrt3\) é uma raiz não exata, pois \(\sqrt{3}=2,449489…\) , que é um número irracional.
Quais são as propriedades da raiz quadrada?
Existem propriedades que podem facilitar o cálculo da raiz quadrada. Vamos conhecer algumas, considerando a e b números reais positivos.
-
A raiz quadrada de um produto é igual ao produto das raízes quadradas.
\(\sqrt{ab}=\sqrt{a}⋅\sqrt b\)
-
A raiz quadrada de uma divisão é igual à divisão das raízes quadradas.
\(\sqrt{\frac{a}{b}}=\sqrt{\frac{a}{b}}\)
-
A raiz quadrada de \(a^m\) é igual à raiz quadrada de a elevada ao expoente m.
\(\sqrt{a^m}=(\sqrt{a})^m\)
-
A raiz quadrada de \(a^2 \) é igual a a.
\(\sqrt{a^2}=a\)
Observação: Definimos essa propriedade para a positivo. Caso a seja um número desconhecido (podendo ser positivo ou negativo), dizemos que \(\sqrt{a^2}=|a|\).
As propriedades são muito úteis para simplificações e para encontrar raízes quadradas de números grandes. Observe o exemplo abaixo.
Exemplo:
Qual o valor de \(\sqrt{1296}\)?
Primeiramente, vamos fatorar o número 1296 em fatores primos:
\(1296=2^4⋅3^4\)
Agora, vamos reescrever utilizando potências de expoente 2:
\(1296=2^2⋅2^2⋅3^2⋅3^2\)
Portanto, aplicando a primeira e a última propriedade, temos que
\(\sqrt{1296}=\sqrt{2^2⋅2^2⋅3^2⋅3^2}=\sqrt{2^2}⋅\sqrt{2^2 }⋅\sqrt{3^2}⋅\sqrt{3^2}= 2 ⋅2⋅3⋅3 = 36\)
Leia também: Como calcular uma raiz quadrada aproximada?
Exercícios resolvidos sobre raiz quadrada
Questão 1
A simplificação da expressão \(\frac{2\sqrt{14}}{\sqrt{7}}\) é
a) \(2\sqrt{3}\)
b) \(2\sqrt{2}\)
c) \(3\sqrt{2}\)
d) \(3\sqrt{3}\)
e) \(\sqrt{2}\)
Resolução
Alternativa B.
Observe que \(\sqrt{14}=\sqrt{2⋅7}\). Aplicando a propriedade, temos que \(\sqrt{2⋅7}=\sqrt{2}⋅\sqrt{7}\).
Portanto,
\(\frac{2\sqrt{14}}{√7}=\frac{2⋅\sqrt{2⋅7}}{√7}=\frac{2⋅\sqrt{2}⋅\sqrt{7}}{\sqrt{7}}=2\sqrt2\)
Questão 2
Sabendo que x é um número real positivo e \(x^2=\frac{5}9\), o valor de 2x é
a) \(\frac{3\sqrt5}{2}\)
b) \(\frac{5\sqrt5}{2}\)
c) \(\frac{3\sqrt2}{5}\)
d) \(\frac{2\sqrt5}{3}\)
e) \(\frac{2\sqrt3}{5}\)
Resolução
Alternativa D.
Se x é positivo, então, aplicando a propriedade da raiz quadrada de uma divisão, temos que
\(x=\sqrt{\frac{5}{9}}=\frac{\sqrt5}{\sqrt9}=\frac{\sqrt5}{3}\)
Assim, 2x é igual a \(\frac{2\sqrt5}{3}\).