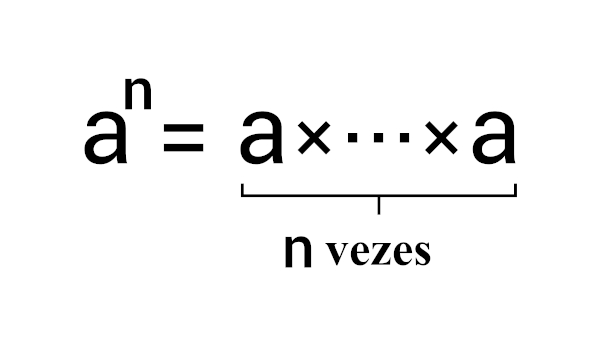A raiz cúbica é o caso particular da radiciação com índice 3. Para encontrar a raiz cúbica de um número x, devemos buscar um número y tal que \(y^3=x\). Se esse processo parecer difícil, podemos empregar a fatoração de x e as propriedades de radiciação como ferramentas, além de estratégias de aproximação e arredondamentos.
Leia também: Raiz quadrada — o caso mais comum de radiciação
Tópicos deste artigo
- 1 - Resumo sobre raiz cúbica
- 2 - Como é a representação da raiz cúbica de um número?
- 3 - Como calcular a raiz cúbica de um número?
- 4 - Como se calcula a raiz cúbica por aproximação?
- 5 - Exercícios resolvidos sobre raiz cúbica
Resumo sobre raiz cúbica
- A representação da raiz cúbica de x é \(\sqrt[3]{x}\).
- A raiz cúbica de x é igual a y se \(y^3=x.\)
- Podemos encontrar uma aproximação para uma raiz cúbica ao determinar intervalos nos quais ela se encontra.
Como é a representação da raiz cúbica de um número?
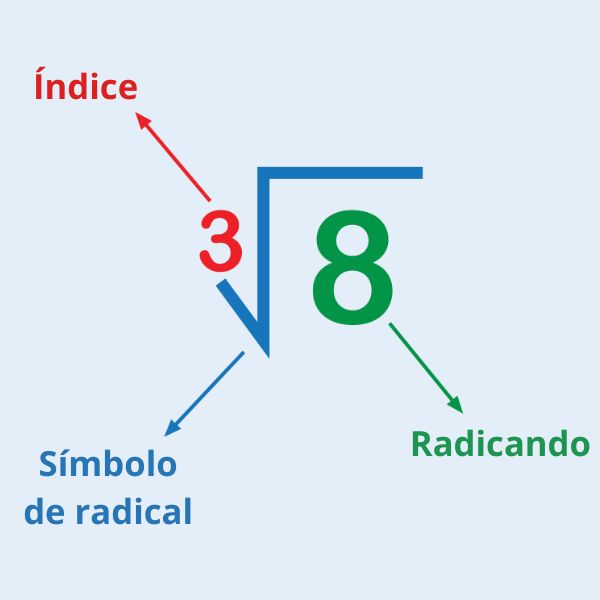
A representação da raiz cúbica de um número é composta por quatro elementos:
- o radicando, que é o número do qual buscamos a raiz;
- a raiz cúbica, que é a resposta procurada;
- o radical, que é o símbolo indicativo da operação de radiciação;
- o índice, que determina o expoente da raiz para resultar no radicando — como estamos considerando uma raiz cúbica, o índice é 3.
Assim, se a raiz cúbica de um número x é igual a um número y, devemos representar da seguinte forma:
\(\sqrt[3]{x}\ =\ y\)
Neste exemplo, x é o radicando, y é a raiz cúbica, \(\sqrt{▢}\) é o radical e 3 é o índice.
Como calcular a raiz cúbica de um número?
Calcular a raiz cúbica de um número x significa procurar um número y tal que \(y^3=x\) . Dependendo do valor de x, pode ser vantajoso realizar a fatoração em números primos. Vejamos alguns exemplos.
Exemplo 1: Qual a raiz cúbica de 64?
Determinar a raiz cúbica de 64 significa procurar um número y tal que \(y^3=64\). Vamos fazer alguns testes com números naturais:
\(1^3=1\ \cdot1\ \cdot1\ =\ 1\)
\(2^3=2\ \cdot2\ \cdot2\ =8\)
\(3^3=3\ \cdot3\ \cdot3\ =27\)
\(4^3=4\cdot4\cdot4=64\)
Portanto, \(\sqrt[3]{64}\ =\ 4\)
Exemplo 2: Qual a raiz cúbica de 2744?
Neste caso, como o radicando é um número maior, vamos utilizar sua representação fatorada.
\(2744=2^3\cdot7^3\)
Portanto, utilizando a propriedade de radiciação:
\(\sqrt[3]{2744}\ =\ \sqrt[3]{2^3\cdot7^3}\ =\ \sqrt[3]{2^3}\ \cdot\sqrt[3]{7^3}\ =\ 2\ \cdot7\ =\ 14\)
Observações:
- Quando a raiz cúbica é um número inteiro, como nos exemplos anteriores, dizemos que o radicando é um cubo perfeito. Outros exemplos de cubos perfeitos são os números 8 (pois 23 = 8, e 2 é inteiro), 27 (pois 33 = 27, e 3 é inteiro) e 125 (pois 53 = 125, e 5 é inteiro).
- Quando a raiz cúbica é um número racional, dizemos que é uma raiz exata.
Como se calcula a raiz cúbica por aproximação?
Nas situações em que for muito complicado ou mesmo impossível determinar um valor exato para a raiz cúbica, podemos utilizar aproximações. Para isso, delimitamos um intervalo no qual a raiz está contida. As extremidades do intervalo devem ser raízes cúbicas cujo valor seja conhecido.
Observação: esse método se baseia no fato de que, quanto maior o radicando, maior o valor da raiz cúbica. Ou seja, se a < b então \(\sqrt[3]{a}\ <\ \sqrt[3]{b}\).
A princípio pode parecer um processo complicado, mas vejamos como isso funciona na prática.
Exemplo: Qual a raiz cúbica de 10? (Utilize uma aproximação com 1 casa decimal.)
Perceba que a raiz cúbica de 10 está entre a raiz cúbica de 8 e a raiz cúbica de 27, que são valores conhecidos:
\(\sqrt[3]{8}\ <\sqrt[3]{10}<\sqrt[3]{27}\)
\(2\ <\sqrt[3]{10}<3\)
Assim, a raiz cúbica de 10 é um número entre 2 e 3. Lembre-se de que \(\sqrt[3]{10}\) é um número y tal que \(y^3=10\). Portanto, vamos calcular algumas possibilidades:
\({2,1}^3=9,261\)
\({2,2}^3=10,648\)
\({2,3}^3=12,167\)
Observe que 2,1 e 2,2 são aproximações para a raiz quadrada de 10. Como 2,13 resulta em um número um pouco abaixo de 10, dizemos que é uma aproximação por falta; já 2,13 é uma aproximação por excesso, pois resulta em um número um pouco acima de 10.
Assim, \(\sqrt[3]{10}\ \approx2,1\) ou \(\sqrt[3]{10}\ \approx2,2\).
Leia também: Como calcular uma raiz quadrada aproximada?
Exercícios resolvidos sobre raiz cúbica
Questão 1
A raiz cúbica de 3375 é
a) 11
b) 12
c) 13
d) 14
e) 15
Resolução
Aplicando a fatoração do radicando 3375 e utilizando a propriedade de radiciação:
\(\sqrt[3]{3375}\ =\ \sqrt[3]{3^3\cdot5^3}\ =\ \sqrt[3]{3^3}\ \cdot\sqrt[3]{5^3}\ =\ 3\ \cdot5\ =\ 15\)
Alternativa E.
Questão 2
O valor aproximado de \(\sqrt[3]{80}\) é
a)4,1
b) 4,3
c) 4,7
d) 5,2
e) 5,6
Resolução
Observe que
\(\sqrt[3]{64}\ <\sqrt[3]{80}<\sqrt[3]{125}\)
\(4\ <\sqrt[3]{80}<5\)
Assim, podemos verificar algumas possibilidades:
\({4,1}^3=68,921\)
\({4,2}^3=74,088\)
\({4,3}^3=79,507\)
\({4,4}^3=85,184\)
\({4,5}^3=91,125\)
Perceba que, se continuarmos o processo, vamos nos afastar cada vez mais do radicando.
Assim, das alternativas apresentadas, o valor que mais se aproxima de \(\sqrt[3]{80}\) é 4,3.
Alternativa B.