Quadriláteros

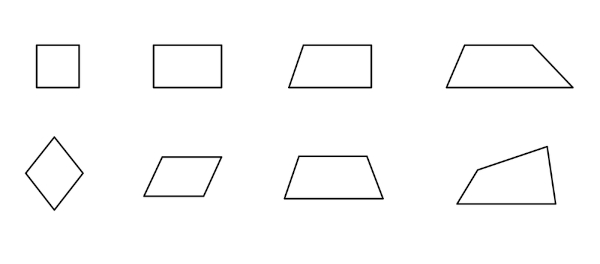
Os quadriláteros são polígonos que possuem 4 lados e podem ser classificados como convexos ou côncavos. Além disso, são compostos por 4 lados, 4 ângulos internos e 4 vértices. A soma dos ângulos internos de um quadrilátero é igual a 360°.

Existem alguns casos especiais de quadriláteros, conhecidos como quadriláteros notáveis, que são: paralelogramo, quadrado, retângulo, losango e trapézio.

Leia também: Principais diferenças entre figuras planas e espaciais

Tópicos deste artigo

• 1 - Resumo sobre os quadriláteros
• 2 - Videoaula sobre quadriláteros
• 3 - O que são quadriláteros?
• 4 - Elementos dos quadriláteros
• 5 - Diferença entre quadrilátero convexo e quadrilátero côncavo
• 6 - Tipos de quadriláteros
  • → Paralelogramos
  • → Trapézio
• 7 - Exercícios resolvidos sobre quadriláteros

Resumo sobre os quadriláteros

• Os quadriláteros são polígonos que possuem 4 lados.

• O quadrilátero pode ser classificado como convexo ou côncavo.

• Um quadrilátero possui 4 lados, 4 vértices, 4 ângulos internos e 2 diagonais.

• A soma dos ângulos internos de um quadrilátero é igual a 360°.

• Existem casos especiais de quadriláteros. São eles:

  • Paralelogramo: quadrilátero com lados opostos paralelos.

  • Quadrado: quadrilátero com lados congruentes e ângulos congruentes.

  • Retângulo: quadrilátero com ângulos congruentes.

  • Losango: quadrilátero com todos os lados congruentes.

  • Trapézio: quadrilátero com dois lados paralelos e dois lados não paralelos.

Videoaula sobre quadriláteros

O que são quadriláteros?

Conhecemos como quadriláteros os polígonos que possuem quatro lados. Um polígono é uma figura plana fechada; quando ele possui 4 lados, é classificado como quadrilátero.

Elementos dos quadriláteros

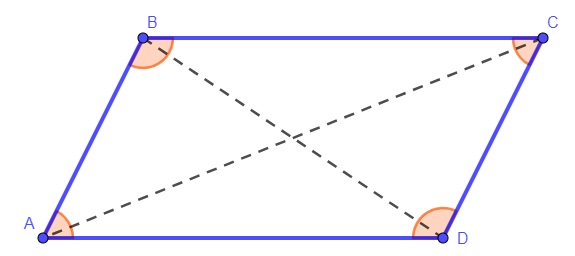
Todo quadrilátero é composto por 4 lados, 4 vértices e 4 ângulos internos. Podemos traçar 2 diagonais.

• Os lados do quadrilátero são os segmentos \(\overline{AB},\overline{AD},\overline{BC},\overline{CD}\).

• Os vértices do quadrilátero são os pontos A, B, C, D.

• Os ângulos internos são \(\hat{A},\hat{B},\hat{C},\hat{D},\) e a soma dos ângulos internos de qualquer quadrilátero é igual a 360°.

• As diagonais do quadrilátero são os segmentos \(\overline{AC}\ e\ \overline{BD}\).

Diferença entre quadrilátero convexo e quadrilátero côncavo

Existem duas classificações possíveis para os quadriláteros: convexo ou côncavo.

• O quadrilátero é convexo quando a medida de cada um dos seus ângulos internos é menor que 180°.

• O quadrilátero é côncavo quando a medida de um dos ângulos internos é maior que 180°.

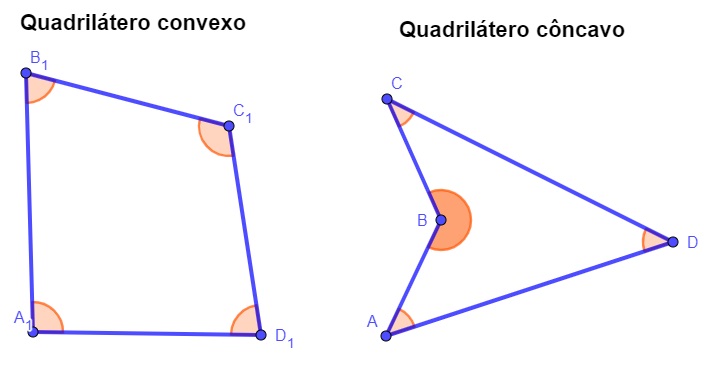
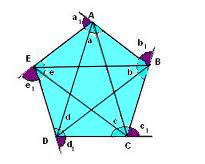
Note que o quadrilátero ABCD possui o ângulo interno \(\hat{B}\) maior que 180°, o que faz com que ele seja um quadrilátero cônvaco. Já o quadrilátero A₁B₁C₁D₁ possui todos os ângulos internos menores que 180°, logo ele é classificado como um quadrilátero convexo.

Tipos de quadriláteros

Alguns quadriláteros recebem nomes especiais devido à sua forma e às suas características. Veja os principais tipos:

→ Paralelogramos

Os paralelogramos são quadriláteros que possuem lados opostos paralelos.

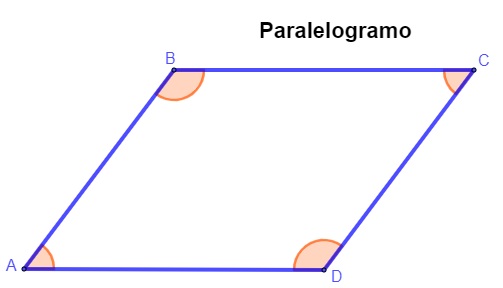
• Os lados \(\overline{AB}\) e \(\overline{CD}\) são opostos e paralelos.

• Os lados \(\overline{AD}\) e \(\overline{BC}\) são opostos e paralelos.

Podemos listar como as principais características de um paralelogramo:

• lados opostos congruentes, ou seja, que possuem a mesma medida;

• ângulos internos opostos congruentes;

• diagonais que se encontram no ponto médio do quadrilátero.

Alguns paralelogramos recebem nomes específicos, devido a características singulares. São eles: o retângulo, o losango e o quadrado.

•  Retângulo

O retângulo é o paralelogramo que possui os quatro ângulos internos retos, ou seja, todos os seus ângulos internos medem 90°.

Note que os lados \(\overline{AB}\) e \(\overline{CD}\) são opostos, paralelos e congruentes. O mesmo acontece quando comparamos os lados \(\overline{AD}\) e \(\overline{CD}\).

•  Losango

O losango também é um caso de paralelogramo. Ele é um quadrilátero que possui todos os lados congruentes, ou seja, todos os seus lados possuem a mesma medida.

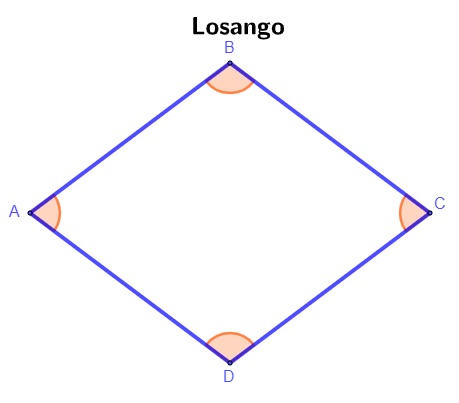
No losango, os lados \(\overline{AB},\overline{BC},\overline{CD}\ e\ \overline{AD}\) são todos congruentes.

•  Quadrado

O quadrado é o paralelogramo que possui todos os ângulos retos e todos os lados congruentes.

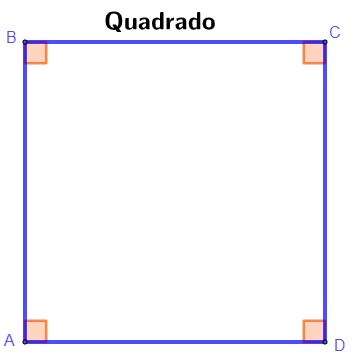
No quadrado, os lados \(\overline{AB},\overline{BC},\overline{CD}\ e\ \overline{AD}\) são congruentes, e cada um dos ângulos \(\hat{A},\hat{B},\hat{C},\hat{D},\) mede 90°.

Note que o quadrado satisfaz a definição de losango e a definição de retângulo, então todo quadrado é um losango, e todo quadrado é um retângulo. Vale ressaltar que a recíproca não é verdadeira, ou seja, nem todo losango é um quadrado, e nem todo retângulo é um quadrado.

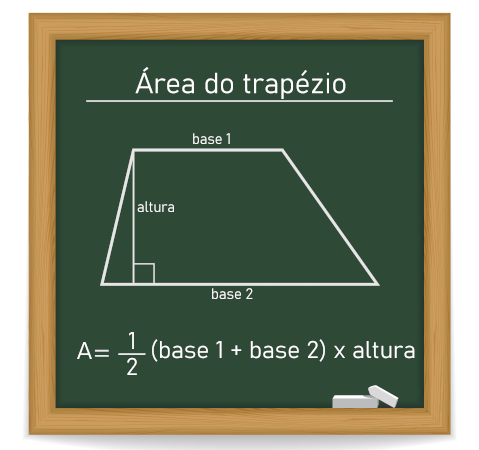
→ Trapézio

O trapézio não é considerado paralelogramo, pois o quadrilátero é classificado como um trapézio quando ele possui dois lados paralelos e dois lados não paralelos. Existem três tipos de trapézio: escaleno, isósceles e retângulo.

• Trapézio escaleno

O trapézio é classificado como escaleno quando ele possui todos os lados com medidas distintas, como na imagem a seguir.

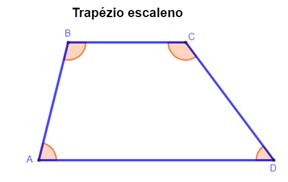
Os lados \(\overline{BC}\) e \(\overline{AD}\) são conhecidos como base menor e base maior do trapézio, respectivamente, e são paralelos entre si.

• Trapézio isósceles

O trapézio é classificado como isósceles quando os lados oblíquos do trapézio são congruentes. Conhecemos como lados oblíquos do trapézio aqueles que não são paralelos. Se eles possuem a mesma medida, então o trapézio é isósceles.

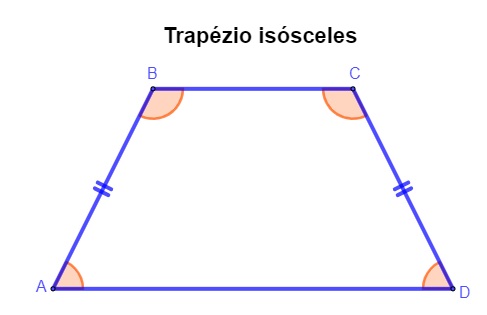
No trapézio, os lados \(\overline{AB}\) e \(\overline{CD}\) são conhecidos como lados oblíquos. Como eles são congruentes, esse trapézio é classificado como isósceles.

• Trapézio retângulo

O trapézio é classificado como trapézio retângulo quando ele possui um de seus ângulos internos reto.

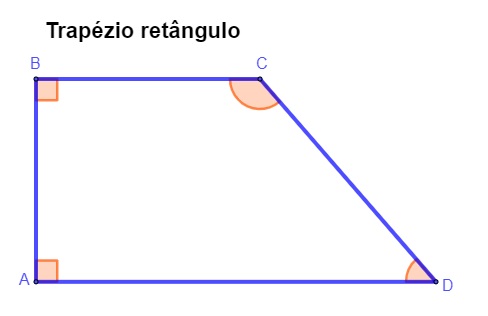
Se um ângulo do trapézio for reto, então ele é considerado um trapézio retângulo. As bases do trapézio são paralelas, então se um ângulo for reto, o outro também será. Assim, o trapézio retângulo possui sempre dois ângulos retos. Note na imagem que os ângulos \(\hat{A}\) e \(\hat{B}\) são ângulos retos.

Leia também: Paralelepípedos — sólidos geométricos cujas faces são todas paralelogramos

Exercícios resolvidos sobre quadriláteros

Questão 1

Um trapézio possui ângulos internos medindo 2x + 5°, 4x + 8°, 50° e x + 17. Podemos afirmar que o valor de x é:

A) 40°

B) 57°

C) 85°

D) 168°

Resolução:

Alternativa A

A soma dos ângulos internos de um quadrilátero é 360°. Logo, temos que:

2x + 5° + 4x + 8° + 50° + x + 17° = 360°

7x + 80° = 360°

7x = 360° - 80°

7x = 280°

x = 280° : 7

x = 40°

Questão 2

(Omni) Qual é a característica comum a todas as três figuras geométricas dadas abaixo?

A) São três quadrados.

B) São três quadriláteros.

C) São três retângulos.

D) São três losangos.

Resolução:

Alternativa B

Analisando a imagem, é possível perceber que as três figuras são quadriláteros. Note que há um quadrado, um retângulo e um paralelogramo, o que exclui as demais alternativas.