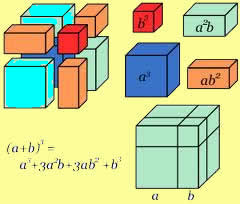Algumas expressões algébricas possuem características comuns ao serem desenvolvidas, elas recebem o nome de produtos notáveis. Esse tipo de expressão respeita uma lógica matemática na sua resolução. Os produtos podem ser resolvidos através da propriedade distributiva da multiplicação ou por uma regra prática. Daremos ênfase à utilização da regra prática, pois através dela reduzimos os cálculos, propiciando dinamismo e praticidade na resolução das situações resolutivas.
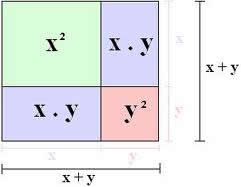
Quadrado da soma: (a + b)² ou (a +b)(a + b)
“O primeiro termo elevado ao quadrado, adicionado ao dobro do primeiro (termo) vezes o segundo (termo), adicionado ao segundo (termo) elevado ao quadrado”.
Exemplo:
(2x + 6)² = (2x)² + 2 * 2x * 6 + (6)² = 4x² + 24x + 36
(9x + 5) = (9x)² + 2 * 9x * 5 + (5)² = 81x² + 91x + 25
(4x² + 3) = (4x²)² + 2 * 4x² * 3 + (3)² = 16x4 + 24x² + 9
(12x + 6y)² = (12x)² + 2 * 12x * 6y + (6y)² = 144x² + 144xy + 36y²
(10x³ + x) = (10x³)² + 2 * 10x³ * x + (x)² = 100x6 + 20x4 + x²
Quadrado da diferença: (a – b)² ou (a – b)(a – b)
“O primeiro termo elevado ao quadrado, subtraído do dobro do primeiro (termo) vezes o segundo (termo), subtraído do segundo (termo) elevado ao quadrado”.
(7x – 8)² = (7x)² – 2 * 7x * 8 + (8)² = 49x² – 112x + 64
(3x – 4)² = (3x)² – 2 * 3x * 4 + (4)² = 9x² – 24x + 16
(6y – 5)² = (6y)² – 2 * 6y * 5 + (5)² = 36y² – 60y + 25
(8a – 7b)² = (8a)² – 2 * 8a * 7b + (7b)² = 64a² – 112ab + 49b²
(12z – 3)² = (12z)² – 2 * 12z * 3 + (3)² = 144z² – 72z + 9
Videoaula relacionada: