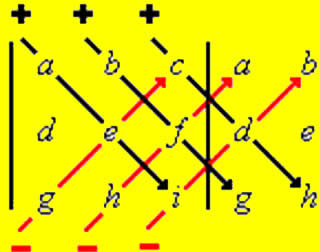
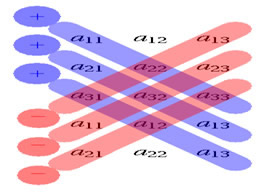
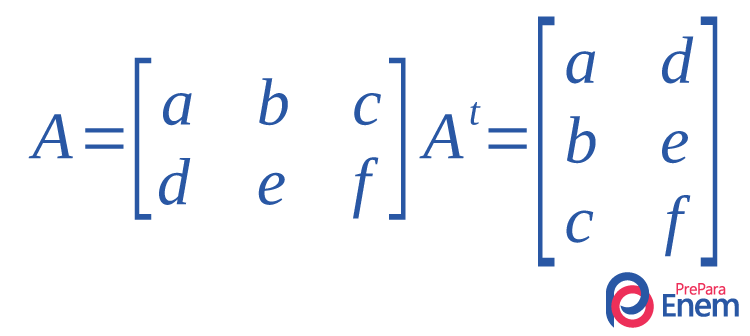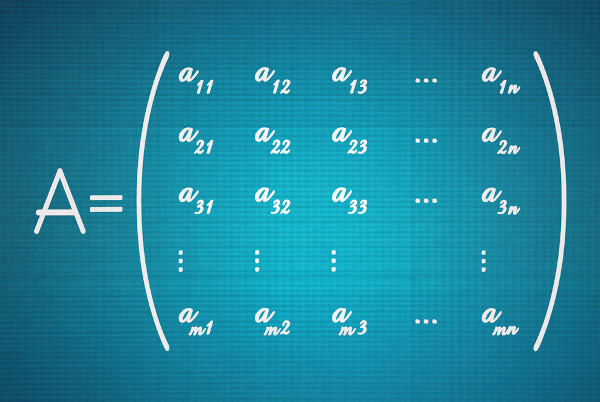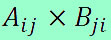O cálculo dos determinantes pode ser facilitado se analisarmos as características e propriedades de algumas matrizes. Há algumas propriedades que, se bem observadas, podem fazer com que economizemos tempo na realização desses cálculos. Vejamos quais são essas propriedades e como elas podem nos ajudar.
Propriedade 1.
Quando todos os elementos de uma linha ou coluna são iguais a zero, o determinante da matriz é nulo.
Exemplo:

Propriedade 2.
Se duas linhas ou duas colunas de uma matriz forem iguais, seu determinante será nulo.
Exemplo:

Propriedade 3.
Se duas linhas ou duas colunas de uma matriz forem proporcionais, então seu determinante será nulo.
Exemplo:

Propriedade 4.
Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.
Exemplo:

Propriedade 5.
Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer, então seu determinante será multiplicado por pm.
det (p?A) = pm?det A
Exemplo:
![]()
Propriedade 6.
O determinante de uma matriz é igual ao determinante de sua transposta.
det A=det At
Exemplo:

Propriedade 7.
Se trocarmos de posição duas linhas ou duas colunas de uma matriz, seu determinante será o oposto da matriz anterior.
Exemplo:

Propriedade 8.
Se os elementos acima ou abaixo da diagonal principal forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.
Exemplo:

Propriedade 9.
O determinante do produto de duas matrizes é igual ao produto dos determinantes de cada uma delas.
det (A?B) = det A ? det B
Propriedade 10.
Teorema de Jacob: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Exemplo:

Se somarmos os elementos da coluna 1 com o dobro dos elementos da coluna 2, o determinante não irá se alterar.

Aproveite pra conferir nossas videoaulas sobre o assunto: