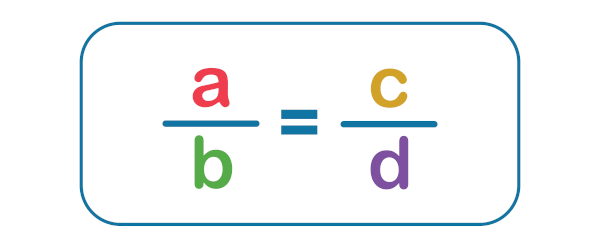Proporção é um conceito presente na Matemática básica que se relaciona à comparação de grandezas, algo muito comum também em outras áreas do conhecimento, como Física, Química e Biologia. Essas grandezas podem se relacionar de forma direta ou inversamente proporcional.
As grandezas são diretamente proporcionais quando, à medida que uma aumenta, a outra também aumenta na mesma proporção, ou quando, à medida que uma diminui, a outra também diminui na mesma proporção. As grandezas são inversamente proporcionais quando, à medida que uma aumenta, a outra diminui na mesma proporção. Utilizamos a proporção e suas propriedades para encontrar valores desconhecidos.
Leia também: Razão entre grandezas diferentes
Tópicos deste artigo
- 1 - Razão e proporção
- 2 - Propriedades da proporção
- 3 - Como calcular uma proporção?
- 4 - Exercícios resolvidos
Razão e proporção
Para analisar se as grandezas são proporcionais ou não, é bastante comum a utilização da razão.
Exemplo:
Verifique se os triângulos são proporcionais.
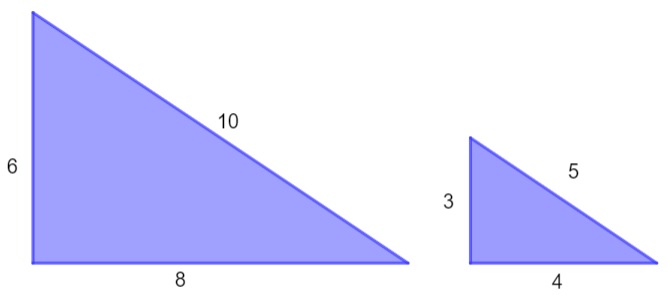
Analisando os triângulos, é possível perceber que eles são proporcionais, pois o maior é o dobro do triângulo menor. Para verificar essa proporção, basta calcular a razão entre os lados.
![]()
Note que a razão entre os lados é sempre a mesma — nesse caso 2 é conhecido como coeficiente de proporcionalidade.
Veja também: Regra de três simples com grandezas diretamente proporcionais
Propriedades da proporção
Para resolver problemas envolvendo proporção, é fundamental conhecer as suas propriedades.
-
1ª propriedade
A propriedade fundamental das proporções é esta: o produto dos meios é igual ao produto dos extremos. A partir dessa propriedade, conseguimos resolver problemas por meio de regra de três, entre outros. Essa é a propriedade mais importante da proporção.
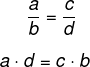
Na proporção, quando há uma igualdade entre frações, ao multiplicar cruzado, sempre encontraremos o mesmo valor. Caso a igualdade seja falsa, ou seja, a multiplicação gere resultados diferentes entre os membros da igualdade, então os valores não são proporcionais.
-
2ª propriedade
Se duas razões são proporcionais, então a soma dos numeradores e dos denominadores também será proporcional às duas razões.
![]()
Exemplo:
![]()
-
3ª propriedade
Se duas razões são proporcionais, então a diferença dos numeradores e dos denominadores também será proporcional às duas razões.
![]()
Exemplo:
![]()
-
4ª propriedade
A soma entre o numerador e o denominador dividida pelo numerador da primeira razão é igual à soma entre o numerador com o denominador dividido pelo numerador da segunda.
Considerando as razões:
![]()
Essa propriedade diz que:
![]()
Exemplo:
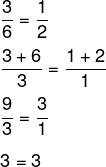
Como calcular uma proporção?
Para utilizar a proporção com o objetivo de encontrar valores desconhecidos, utilizamos a primeira propriedade, conhecida como propriedade fundamental da proporção. Porém, para montar as proporções, é necessário verificar a relação entre essas grandezas. Quando elas são proporcionais, há duas possibilidades: elas podem ser direta ou inversamente proporcionais.
-
Grandezas diretamente proporcionais
Duas ou mais grandezas são diretamente proporcionais quando, à medida que o valor de uma dessas grandezas aumenta, a outra também aumenta na mesma proporção. Essa relação se aplica a várias situações no nosso dia a dia. Em um campeonato de pontos corridos, por exemplo, a quantidade de vitórias e os pontos adquiridos são diretamente proporcionais, ou seja, quanto mais o time vencer, mais pontos ele vai adquirir no campeonato.
Exemplo:
Ao colocar 12 litros de etanol em um veículo, foi possível percorrer 102 km. Sabendo que no tanque desse veículo cabem exatamente 40 litros, qual é a quantidade de km que podemos percorrer?
Sabemos que as grandezas são diretamente proporcionais, pois, se eu aumento a quantidade de combustível do veículo, consequentemente aumento a quantidade de quilômetros. Desse modo, montaremos as razões com as mesmas grandezas, sendo x a quantidade de quilômetros que podem ser percorridos com 40 litros: 12/40 = 102/x.
Aplicando a propriedade fundamental da proporção, temos que:
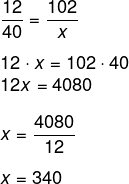
Resultado: 340 km.
-
Grandezas inversamente proporcionais
Duas grandezas são inversamente proporcionais quando, à medida que o valor de uma dessas grandezas aumenta, o valor da outra diminui na mesma proporção. Um exemplo disso é a relação entre a velocidade e o tempo gasto em um percurso fixo. Sabemos que, quanto maior a velocidade, menor será o tempo gasto no percurso. De forma análoga, quanto menor a velocidade, maior será o tempo gasto no percurso.
Exemplo:
Para encher um reservatório, 3 torneiras com a mesma vazão levam exatamente 15 horas para preencher o tanque todo. Em quanto tempo o tanque encheria se fossem 5 torneiras de mesma vazão?
Tratando o valor desconhecido como x e sabendo que, quanto maior a quantidade de torneiras, menor será o tempo gasto, identificamos que se trata de grandezas inversamente proporcionais. Para resolver o problema, vamos montar a razão 3/5 e 15/x. Como os valores são inversamente proporcionais, vamos inverter a segunda fração e resolver utilizando a propriedade fundamental da proporção.
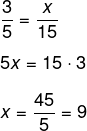
Acesse também: Divisão proporcional: como calcular?
Exercícios resolvidos
Questão 1 — (Enem 2015) Um pesquisador, ao explorar uma floresta, fotografou uma caneta de 16,8 cm de comprimento ao lado de uma pegada. O comprimento da caneta ( c ), a largura (L) e o comprimento (C ) da pegada, na fotografia, estão indicados no esquema
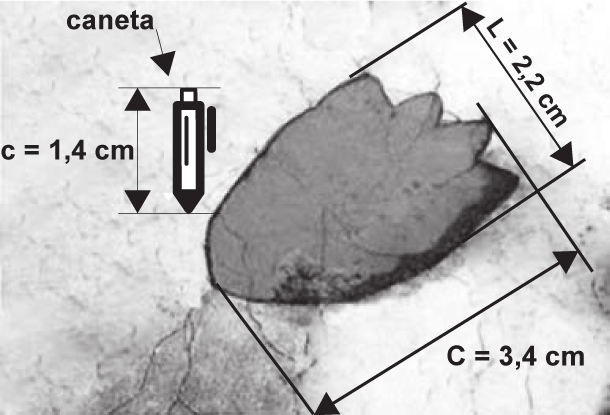
A largura e o comprimento reais da pegada, em centímetros, são, respectivamente, iguais a
A) 4,9 e 7,6
B) 8,6 e 9,8
C) 14,2 e 15,4
D) 26,4 e 40,8
E) 27,5 e 42,5
Resolução
Alternativa D.
Sabemos que os comprimentos são proporcionais, então basta montar a razão entre o comprimento da caneta no desenho e o real, e a largura do desenho com a largura real. Também faremos o mesmo para encontrar o comprimento real. Após montar a razão, aplicaremos a propriedade fundamental da proporção.
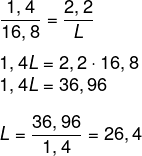
Agora calcularemos o comprimento C.
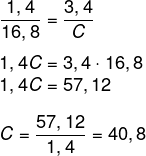
Questão 2 – (Enem 2010) A relação da resistência elétrica com as dimensões do condutor foi estudada por um grupo de cientistas por meio de vários experimentos de eletricidade. Eles verificaram que existe proporcionalidade entre:
-
resistência (R) e comprimento (ℓ ), dada a mesma secção transversal (A);
-
resistência (R) e área da secção transversal (A), dado o mesmo comprimento (ℓ) comprimento (ℓ);
-
área da secção transversal (A), dada a mesma resistência (R).
Considerando os resistores como fios, pode-se exemplificar o estudo das grandezas que influem na resistência elétrica utilizando as figuras seguintes.
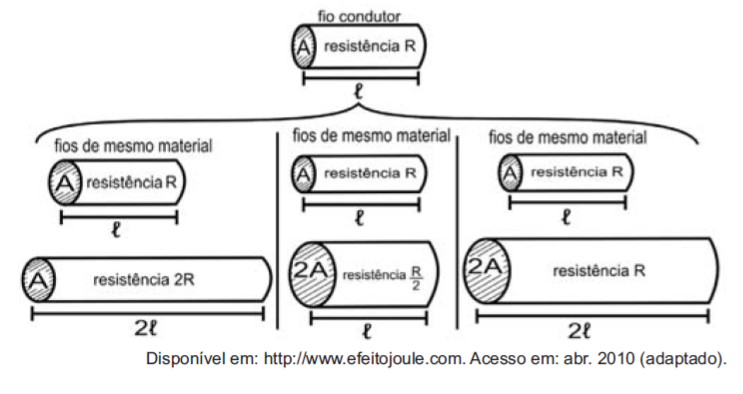
As figuras mostram que as proporcionalidades existentes entre resistência (R) e comprimento (ℓ), resistência (R) e área da secção transversal (A), e entre comprimento (ℓ) e área da secção transversal (A) são, respectivamente:
A) direta, direta e direta.
B) direta, direta e inversa.
C) direta, inversa, direta.
D) inversa, direta e direta.
E) inversa, direta e inversa.
Resolução
Alternativa C.
-
A primeira comparação é entre comprimento e resistência. Note que o comprimento ℓ e a resistência R dobraram na primeira comparação, logo são grandezas diretamente proporcionais.
-
A segunda comparação é entre resistência R e área da secção transversal A. Note que, à medida que A dobrou, R foi dividido por dois, logo essas grandezas são inversamente proporcionais.
-
Na terceira comparação, entre a área de secção transversal A e o comprimento ℓ, à medida que A dobrou, ℓ também dobrou, logo essas grandezas são diretamente proporcionais.
As comparações são direta, inversa e direta, respectivamente.