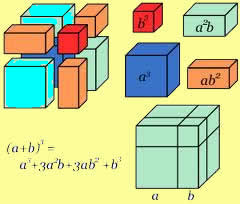Alguns cálculos algébricos possuem uma forma padronizada de respostas e podem ser resolvidos através de situações generalizadas. Os produtos notáveis podem ser resolvidos aplicando algumas generalizações que serão expostas a seguir:
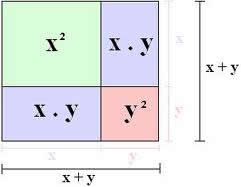
Quadrado da soma
Podemos expressar o quadrado da soma pela generalização (x+y)² ou (x+y)(x+y).
O cálculo (x+y)(x+y) pode ser resolvido aplicando a propriedade distributiva da multiplicação. Temos:
x*x + xy + yx + y*y = x² + 2xy + y²
Regra prática
“O quadrado do primeiro termo mais duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo”.
Quadrado da diferença
Generalizando temos (x-y)² ou (x-y)(x-y):
x*x – xy – yx + y*y = x² – 2xy + y²
Regra prática
“O quadrado do primeiro termo menos duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo”.
Produto da soma pela diferença
Generalizando temos (x+y)(x-y):
x*x – xy + yx – y*y = x² – y²
Regra prática
“Quadrado do primeiro termo menos o quadrado do segundo termo”.
Cubo da soma
Generalizando temos (x+y)³ ou (x+y)*(x+y)*(x+y):
(x² + xy + xy + y²) (x+y)
(x² + 2xy + y²) (x+y)
x³ + x²y + 2x²y + 2xy² + xy² + y³
x³ + 3x²y + 3xy² + y³
Regra prática
“O cubo do primeiro termo mais três vezes o quadrado do primeiro termo vezes o segundo termo, mais três vezes o primeiro termo vezes o quadrado do segundo termo, mais o cubo do segundo termo”.
Cubo da diferença
Generalizando temos (x–y)³ ou (x– y)*(x– y)*(x– y):
(x² – xy – xy + y²) (x–y)
(x² – 2xy + y²) (x–y)
x³ – x²y – 2x²y + 2xy² + xy² – y³
x³ – 3x²y + 3xy² – y³
“O cubo do primeiro termo menos três vezes o quadrado do primeiro termo vezes o segundo termo, mais três vezes o primeiro termo vezes o quadrado do segundo termo, menos o cubo do segundo termo”.
Aproveite para conferir nossa videoaula sobre o assunto: