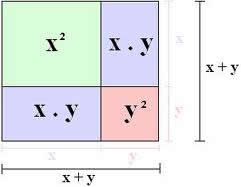
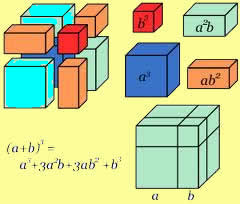Os produtos notáveis são polinômios que possuem uma forma geral para realizar a sua resolução. Eles são utilizados para simplificar problemas envolvendo multiplicação de polinômios. Conhecer a forma de resolução de cada um dos cinco produtos notáveis facilita na resolução de situações-problemas que envolvem polinômios, que são bastante comuns na geometria analítica e outras áreas da Matemática.
Os cinco produtos notáveis são:
-
quadrado da soma;
-
quadrado da diferença;
-
produto da soma pela diferença;
-
cubo da soma;
-
cubo da diferença.
Vale ressaltar que estudar produtos notáveis é encontrar um método para resolver, de forma mais rápida, cada um desses casos citados.
Leia também: Como calcular a divisão de polinômios?
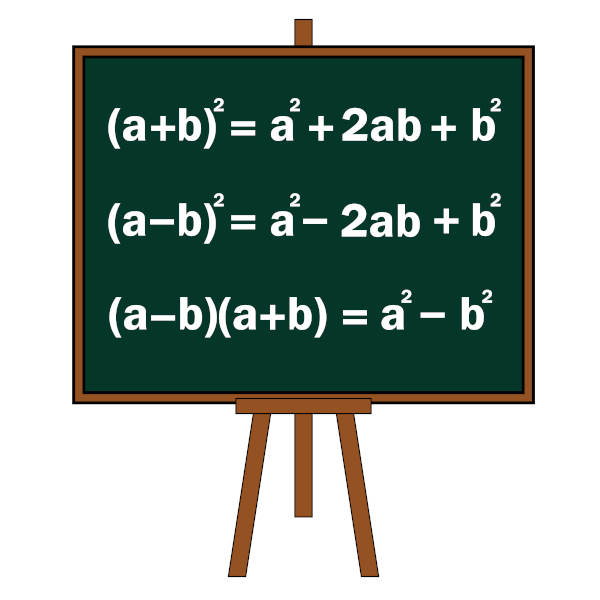
Tópicos deste artigo
- 1 - Quais são os produtos notáveis?
- 2 - Produtos notáveis e fatoração de polinômios
- 3 - Exercícios resolvidos
Quais são os produtos notáveis?
Para resolver multiplicações cujos termos são polinômios, é necessário saber diferenciar cada um dos casos de produtos notáveis. Atualmente eles são divididos em cinco, e cada um possui um método de resolução. São eles: quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença.
-
Quadrado da soma
Como o nome sugere, estamos elevando uma soma de dois termos ao quadrado, como nos exemplos a seguir.
Exemplos:
-
(x + y) ²
-
(a + b) ²
-
(2x + 3y)²
-
(x + 2)²
Quando o polinômio possui dois termos, como nos exemplos, estamos trabalhando com um binômio. Elevar um binômio ao quadrado nada mais é do que multiplicá-lo por ele mesmo; porém, para que não seja necessário repetir esse processo sempre, basta lembrar que ele é um produto notável e que, nesse caso, existe um jeito prático de resolver.
(a + b) ² = a ² + 2ab + b²
Sabendo que a é o primeiro termo e b é o segundo termo, para resolver o quadrado da soma, basta lembrar sempre que a resposta será:
-
a² (quadrado do primeiro termo);
-
+ 2ab (mais duas vezes o primeiro termo vezes o segundo termo);
-
+ b² (mais o quadrado do segundo termo).
Exemplo 1:
(x + 3) ²
x → primeiro termo
3 → segundo termo
Assim, podemos escrever:
-
quadrado do primeiro termo → x²;
-
mais duas vezes o primeiro termo vezes o segundo termo → 2·x·3 = 6x;
-
mais o quadrado do segundo termo → 3² = 9.
Logo, podemos dizer que:
(x+3)² = x² + 6x + 9
Exemplo 2:
(2x + 3y)²
Podemos escrever:
-
quadrado do primeiro termo → (2x)² = 4x²;
-
mais duas vezes o primeiro termo vezes o segundo termo → (2·2x·3y) = +12xy;
-
mais o quadrado do segundo termo → (3y)² = 9y².
(2x + 3y)² = 4x² + 12xy + 9y²
Leia também: Multiplicação de fração algébrica – como calcular?
-
Quadrado da diferença
O jeito de resolver não é muito diferente do quadrado da soma, logo, se você compreendeu bem o quadrado da soma, não terá dificuldade em compreender o quadrado da diferença também. Nesse caso, vamos ter, ao invés da soma, uma diferença entre dois termos ao quadrado.
Exemplos:
-
(x – y) ²
-
(a – b) ²
-
(5x – 3y)²
-
(y – 4)²
Nesse caso, temos que:
(a – b) ² = a ² – 2ab + b²
Note que, ao comparar o quadrado da soma e o quadrado da diferença, o que muda é somente o sinal do segundo termo.
Sabendo que a é o primeiro termo e b é o segundo termo, para resolver o quadrado da diferença, basta lembrar que a resposta será:
-
a² (quadrado do primeiro termo);
-
– 2ab (menos duas vezes o primeiro termo vezes o segundo termo);
-
+ b² (mais o quadrado do segundo termo).
Exemplo 1:
(y – 4) ²
y → primeiro termo
4 → segundo termo
Podemos escrever, portanto:
-
quadrado do primeiro termo → y²;
-
menos duas vezes o primeiro termo vezes o segundo termo → - 2 · y · 4 = -8y;
-
mais o quadrado do segundo termo → 4² = 16.
Então, temos que:
(y – 4) ² = y² – 8y + 16
-
Produto da soma pela diferença de dois termos
Outro caso de produto notável bastante comum é o cálculo do produto da soma com a diferença de dois termos.
(a + b) ( a – b) = a² – b²
(a + b) → soma
(a – b) → diferença
Nesse caso, temos que:
-
a→ primeiro termo
-
b → segundo termo
Então, (a + b) (a – b) será igual a:
-
a² (quadrado do primeiro termo);
-
-b² (menos o quadrado do segundo termo).
Exemplo:
(x + 5 ) ( x – 5 )
x → primeiro termo
5 → segundo termo
Podemos escrever:
-
quadrado do primeiro termo → x²;
-
menos o quadrado do segundo termo → - 5² = - 25.
Então, temos que:
(x + 5 ) ( x – 5 ) = x² – 25
Leia também: Como encontrar o MMC de polinômios?
-
Cubo da soma
É possível também desenvolver uma fórmula para calcular o cubo da soma.
(a + b)³ = a³ + 3a²b + 3ab² + b³
Assim, temos que:
-
a→ primeiro termo;
-
b → segundo termo
-
a³ → cubo do primeiro termo;
-
+3a²b → mais três vezes o quadrado do primeiro termo vezes o segundo termo;
-
+3ab² → mais três vezes o primeiro termo vezes o quadrado do segundo termo;
-
+b³ → mais o cubo do segundo termo.
Exemplo:
(x + 2)³
Podemos escrever:
-
cubo do primeiro termo → x³;
-
mais três vezes o quadrado do primeiro termo vezes o segundo termo → 3·x²·2 = + 6x²;
-
mais três vezes o primeiro termo vezes o quadrado do segundo termo → 3·x·2² = 3·x·4=12x;
-
mais o cubo do segundo termo → 2³ = +8.
Então, temos que:
(x+2)³ = x³ + 6x² + 12x + 8
Note que esse caso é um pouco mais complexo do que o quadrado da soma e, quanto maior for o expoente, mais difícil será de resolver.
-
Cubo da diferença
A diferença entre o cubo da diferença e o cubo da soma é só no sinal dos termos.
(a – b)³ = a³ – 3a²b + 3ab² - b³
Assim, temos que:
-
a³ → cubo do primeiro termo;
-
– 3a²b → menos três vezes o quadrado do primeiro termo vezes o segundo termo;
-
+3ab² → mais três vezes o primeiro termo vezes o quadrado do segundo termo;
-
– b³ → menos o cubo do segundo termo.
Exemplo:
(x – 2)³
Assim sendo, temos que:
-
cubo do primeiro termo → x³;
-
menos três vezes o quadrado do primeiro termo vezes o segundo termo → 3·x²·2 = – 6x²;
-
mais três vezes o primeiro termo vezes o quadrado do segundo termo → 3·x·2² = 3·x·4=12x;
-
mais o cubo do segundo termo → 2³ = – 8.
(x – 2)³= x³ – 6x² + 12x – 8.
Produtos notáveis e fatoração de polinômios
Existe uma relação muito próxima entre os produtos notáveis e a fatoração de polinômios. Para realizar simplificações, em vez de desenvolver o produto notável, muitas vezes temos a necessidade de fatorar a expressão algébrica, escrevendo-a como um produto notável. Nesse caso, é essencial conhecer os produtos notáveis para que seja possível realizar essas simplificações.
Fatorar nada mais é do que transformar o polinômio no produto dos seus termos. Em caso de fatoração de um polinômio que é um produto notável, seria como realizar a operação contrária de desenvolver esse produto notável.
Exemplo:
Fatore o polinômio x² – 16.
Analisando esse polinômio, queremos escrevê-lo como a multiplicação de dois termos, mas, se analisarmos bem, podemos reescrevê-lo da seguinte maneira:
x² – 4²
Nesse caso, temos o quadrado do primeiro termo menos o quadrado do segundo termo. O produto notável que, ao ser desenvolvido, gera essa expressão algébrica é o produto da soma pela diferença de dois termos. Assim, podemos fatorar essa expressão reescrevendo-a da seguinte maneira:
x² – 16 = (x + 4) (x – 4)
Exercícios resolvidos
Questão 1 – A área do retângulo a seguir pode ser representada pelo polinômio:

A) x – 2.
B) x² – 4.
C) x² + 2.
D) x + 4.
E) x³ – 8.
Resolução
Alternativa B.
A área de um retângulo é a multiplicação da sua base pela altura, então:
A = (x + 2 ) ( x – 2)
Note que esse é um produto notável: produto da soma pela diferença.
A = (x + 2 ) ( x – 2) = x² – 4
Questão 2 – Simplificando a expressão (x + 3 )² – (x + 3) ( x – 3 ) - 6x, encontraremos:
A) 0.
B) x³ – 18.
C) 2x².
D) x² + 9.
E) 18.
Resolução
Alternativa E.
Nesse caso, temos dois produtos notáveis e resolveremos cada um deles.
(x+3)² = x² + 6x + 9
(x + 3) ( x – 3) = x² – 9
Então, temos que:
x² + 6x + 9 – (x² – 9) -6x
x² + 6x + 9 – x² + 9 – 6x
x² – x² 6x – 6x + 9 + 9
18