Produto notável: Soma pela diferença de dois termos

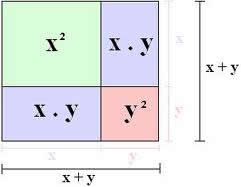
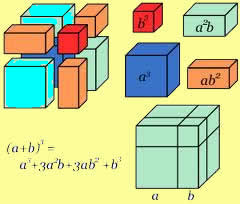Os produtos notáveis são produtos que envolvem expressões algébricas que resultam em um padrão algébrico, ou seja, possuem uma regularidade em seus resultados, tornando não necessário o processo de multiplicação algébrica, podendo sempre utilizar o resultado pela regularidade.

Neste artigo, poderá ser estudado o produto notável da soma pela diferença de dois termos. Para isso será realizado o cálculo por dois processos, o algébrico e o geométrico; contudo, em ambos os casos teremos expressões algébricas a serem resolvidas.

O intuito de passar por esses dois casos é para que possamos ver que todas essas letras representando números possuem aplicabilidade, neste caso utilizaremos no cálculo da área de retângulos.

Pelo título, podemos notar que teremos o produto da soma pela diferença de dois termos, portanto, denotaremos esses dois termos por um número qualquer, ou seja, por uma letra que representará qualquer número que exista. Utilizaremos as letras a e b. Sendo assim, devemos somar esses dois números e multiplicá-los pela diferença dos mesmos dois números. Ou seja:

Portanto, devemos desenvolver esse produto e encontrar a regularidade dessa multiplicação, um resultado que será sempre verdade quando tivermos dois termos, um sendo somado e outro sendo subtraído.

Para realizarmos este produto deveremos aplicar a propriedade da multiplicação, a propriedade distributiva.

Veja que a soma e a diferença são dos mesmos termos, que na expressão final o sinal negativo ficou no termo que estava subtraindo, ou seja, (-b).

Enquanto isso, por meio da imagem abaixo, veremos que essa expressão algébrica pode ser representada através do cálculo da área de um retângulo.

Veja que para encontrarmos a área do Retângulo ABCD devemos realizar o seguinte produto:

Entretanto, podemos calcular as áreas dos retângulos ABFE e CDEF e somá-las, esta expressão nos dará a área do retângulo ABCD.

Sendo assim, devemos somar estas áreas.

Como foi dito inicialmente, a soma dessas áreas resultaria na área do retângulo ABCD, portanto, podemos igualar as expressões.

Videoaula relacionada: