Figuras geométricas podem ser classificadas como planas ou espaciais. Nesse último caso, as figuras são chamadas de sólidos geométricos. Essa classificação é feita de acordo com o número de dimensões necessárias para construção e definição da figura, portanto, para compreender as diferenças entre figuras planas e espaciais, é preciso saber inicialmente o que são as dimensões do espaço e quais figuras podem ser definidas nelas.
Dimensões do espaço
Um ponto é uma figura geométrica que não possui dimensão, tamanho ou forma. Assim, dizemos que o ponto tem número de dimensões igual a zero, ou que o ponto é uma figura adimensional.
A reta é uma figura geométrica que possui número de dimensões igual a 1. Isso pode ser observado da seguinte maneira: as retas apresentam comprimento infinito, mas não têm largura ou profundidade. Além disso, as retas podem ser compreendidas também como o “espaço unidimensional” dentro do qual todas as figuras que possuem uma dimensão ou menos podem ser construídas.
As figuras que têm uma dimensão são: a própria reta, segmentos de reta e semirretas. Além dessas figuras, apenas o ponto pode ser encontrado dentro de uma reta, quando ela é compreendida como espaço unidimensional.
A figura a seguir mostra uma tentativa de construir um quadrado dentro de um espaço unidimensional – uma reta. Como o quadrado é uma figura bidimensional, é impossível defini-lo dentro de um espaço que possui menos de duas dimensões.
Figuras planas
Figuras bidimensionais são aquelas que necessitam de um espaço bidimensional para serem construídas.
O plano é uma figura geométrica que tem número de dimensões igual a 2. Assim, os planos possuem tanto comprimento quanto largura infinitos, mas não têm profundidade. O plano é o “espaço bidimensional”, ou seja, qualquer figura bidimensional precisa de, no mínimo, um plano para ser construída.
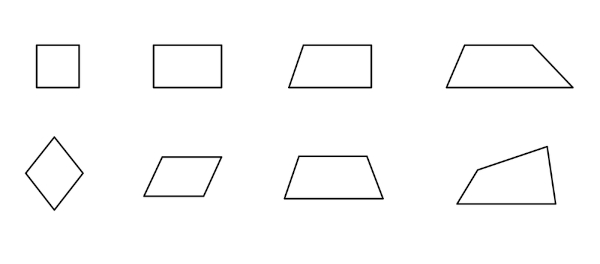
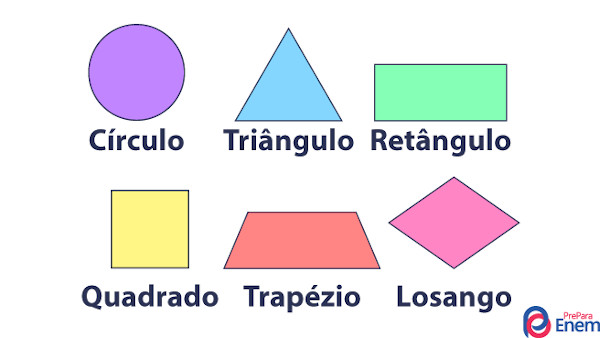
Assim, figuras bidimensionais também são chamadas de figuras planas. São exemplos dessas figuras: quadrados, triângulos, retângulos, círculos etc. Portanto, a figura plana é toda aquela que apresenta comprimento e largura, mas não possui profundidade. A imagem a seguir mostra alguns exemplos de figuras planas.

Figuras espaciais
Figuras tridimensionais são aquelas que necessitam de um espaço tridimensional para serem construídas. Se tentarmos encaixar um cubo dentro de um plano, por exemplo, certamente perceberemos que a maior parte desse cubo ficará fora do plano. Isso acontece porque o cubo é tridimensional e o plano é bidimensional.
O lugar ou “espaço” onde as figuras tridimensionais podem ser construídas é também chamado de espaço. Dentro dele, é possível construir figuras que possuem largura, comprimento e profundidade. Isso porque o espaço em si é uma figura geométrica que tem largura infinita, assim como comprimento e profundidade, também infinitos. Então, ele é considerado o “espaço tridimensional”.
Sendo assim, qualquer figura que precisa de três dimensões para ser construída e definida é chamada de figura geométrica espacial.
São exemplos de figuras espaciais: cubo, prisma, paralelepípedo, pirâmide, cone, cilindro, esfera etc.
Videoaulas relacionadas: