O plano cartesiano pode representar duas retas no plano de acordo com as seguintes posições: concorrentes ou paralelas. Essas posições são determinadas de acordo com a lei de formação de cada função do 1º grau, visto que essas funções possuem como representação geométrica uma reta. Os coeficientes angulares das retas determinam o posicionamento decorrente delas. Por exemplo:
Coeficientes angulares iguais geram retas paralelas.
Coeficientes angulares diferentes geram retas concorrentes.
O coeficiente angular de uma reta corresponde ao ângulo formado entre a reta da função e o eixo das abscissas. Na lei de formação, temos que o coeficiente angular é representado pelo valor do coeficiente de x. Por exemplo:
y = 2x + 6, coeficiente angular: 2
y = –4x + 3, coeficiente angular: –4
Retas Paralelas
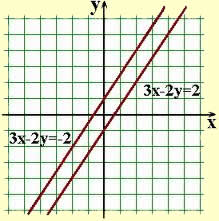
As funções y = 3x – 1 e y = 3x + 2 formam retas paralelas em razão da igualdade decorrente de seus coeficientes angulares. Observe o gráfico:

Retas Concorrentes
Temos que as funções y = 2x + 1 e y = 4x + 3 são concorrentes, pois os valores dos coeficientes angulares são diferentes. Observe o gráfico.

Videoaula relacionada: