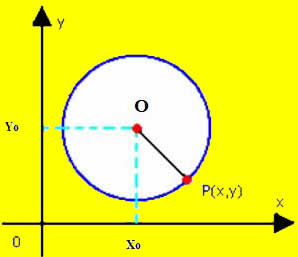
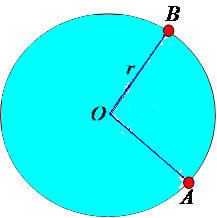
Sabemos que os pontos de uma circunferência estão a uma mesma distância do centro O(x0, y0) e que a essa distância damos o nome de raio. Se um ponto P(xP ,yP) do plano não pertence à circunferência, a distância do centro até ele é maior ou menor que o raio. Se a distância entre O e P for maior que o raio, podemos afirmar que P é exterior à circunferência. Se a distância entre O e P for menor que o raio, então P é interior à circunferência.
Vamos analisar cada situação.
1º caso: P(xP, yP) é um ponto da circunferência.

Se P é um ponto da circunferência, então dP,O = r
2º caso: P(xP, yP) é um ponto exterior à circunferência.
.jpg)
Se P é um ponto exterior à circunferência, então dP,O > r
3º caso: P(xP, yP) é um ponto interior à circunferência.

Se P é um ponto interior à circunferência, então dP,O < r
Exemplo 1. Dada uma circunferência de equação (x – 5)2 + (y – 4)2 = 25, verifique a posição relativa do ponto P(9, 7) em relação à circunferência dada.
Solução: Devemos calcular a distância entre o ponto P e o centro O e verificar se é maior, menor ou igual à medida do raio da circunferência.
Da equação reduzida da circunferência, temos:
x0 = 5 e y0 = 4 → O(5, 4)
r2 = 25 → r = 5
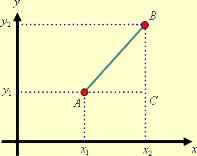
Vamos determinar a distância entre P e O, utilizando a fórmula da distância entre dois pontos.

Como a distância entre o centro O da circunferência e o ponto P é igual à medida do raio, podemos afirmar que P(9, 7) pertence à circunferência.
Exemplo 2. Verifique a posição relativa entre o ponto P(2, – 5) e a circunferência de equação (x – 2)2 + (y – 3)2 = 49.
Solução: Devemos verificar se a distância entre o ponto P e o centro O é maior, menor ou igual à medida do raio. Da equação da circunferência, obtemos:
x0 = 2 e y0 = 3 → O(2, 3)
r2 = 49 → r = 7
Vamos calcular a distância entre P e O, utilizando a fórmula da distância entre dois pontos.

Como a distância entre P e O é maior que a medida do raio, podemos afirmar que o ponto P(2,– 5) é exterior à circunferência.
Exemplo 3. Dada uma circunferência de equação x2 + y2 = 144 e um ponto P(0, – 7). Podemos afirmar que P é um ponto da circunferência?
Solução: Para verificar se P é um ponto da circunferência devemos calcular a distância de O até P e verificar se é igual à medida do raio. Da equação reduzida da circunferência, obtemos:
x0 = 0 e y0 = 0 → O(0, 0)
r2 = 144 → r = 12
Vamos obter a distância entre P e O, utilizando a fórmula da distância entre dois pontos.

Como a distância entre P e O é menor que a medida do raio, P(0, – 7) é interior à circunferência e não um ponto da circunferência.
Videoaula relacionada: