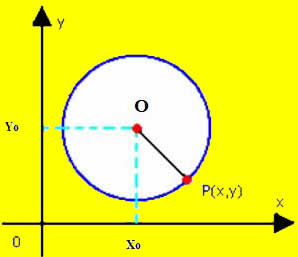
Considere uma circunferência no plano de cento O(xo, yo) e raio r. Dada uma reta s de equação ax + by +c = 0, também do mesmo plano. A reta s pode ser tangente, secante ou externa à circunferência. Se s for tangente, ela toca a circunferência em um só ponto. Se s for secante, intercepta a circunferência em dois pontos distintos. E se for externa à circunferência, a reta s não possui nem um ponto em comum com a circunferência.
Do ponto de vista de geometria analítica, temos:
1º caso: A reta s é externa à circunferência.

Nesse caso, a distância entre o centro O e a reta s é maior que a medida do raio. Ou seja:
dO,s > r
2º caso: A reta s é tangente à circunferência.

Nesse caso, a distância entre o centro O e a reta s é exatamente igual ao raio. Ou seja:
dO,s = r
3º caso: A reta s é secante à circunferência.

Nesse caso, a distância entre o centro O e a reta s é menor que a medida do raio. Ou seja:
dO,s < r
Exemplo 1. Verifique a posição relativa entre a reta s: 3x + y – 13 = 0 e a circunferência de equação (x – 3)2 + (y – 3)2 = 25.
Solução: Devemos calcular a distância entre o centro da circunferência e a reta s e comparar com a medida do raio. Da equação da circunferência, obtemos:
x0 = 3 e y0 = 3 → O(3, 3)
r2 = 25 → r = 5
Vamos utilizar a fórmula da distância entre ponto e reta para calcular a distância entre O e s.

Da equação geral da reta, obtemos:
a = 3, b = 1 e c = – 13
Assim,
Como a distância entre o centro O e a reta s é menor que o raio, a reta s é secante à circunferência.
Exemplo 2. Verifique se a reta s: 2x + y + 2 = 0 é tangente à circunferência de equação (x – 1)2 + (y – 1)2 = 5.
Solução: Devemos verificar se a distância do centro da circunferência até a reta s é igual à medida do raio. Da equação da circunferência, temos que:
x0 = 1 e y0 = 1 → O(1, 1)
r2 = 5 → r = √5
E da equação da reta, obtemos:
a = 2, b = 1 e c = 2
Vamos aplicar a fórmula da distância entre ponto e reta.

Como a distância entre o centro O e a reta s é exatamente igual à medida do raio, podemos afirmar que a reta s é tangente à circunferência.