Ponto, reta, plano e espaço são os nomes dados a conceitos matemáticos intuitivos que não possuem definição e que dão as bases necessárias para a construção da Geometria. Embora não possuam definição, esses conceitos podem ser discutidos e explicados a partir de algumas de suas características e também do seu uso e de sua importância para a Geometria.
Ponto
Os pontos não possuem definição e é impossível tomar qualquer medida sobre um ponto, pois ele não possui dimensão alguma. Um objeto que não possui dimensão é o que dá maior precisão às localizações no espaço. Por exemplo, se um ponto fosse redondo, em que parte dessa figura seria, precisamente, determinada localização sobre um mapa?
Sendo assim, muitas vezes os pontos são compreendidos como localizações no espaço, e é essa ideia que dá bases para a geometria analítica.
Reta
As retas são compreendidas como conjuntos de pontos. Geometricamente, uma reta é uma linha que não faz curva. Com isso, podemos imaginar que as retas são uma sequência de pontos enfileirados que não fazem curva alguma e sem que haja buracos entre esses pontos.
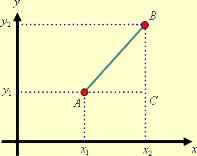
Note que, tomados dois pontos quaisquer sobre uma reta, podemos definir que:
-
Existem infinitos pontos entre eles;
-
É possível medir a distância entre eles;
-
É impossível medir a largura do intervalo entre os pontos, somente o seu comprimento, que é a distância entre os dois pontos.
Sendo assim, dizemos que a reta é uma “figura geométrica” unidimensional (possui uma única dimensão).

Segmento de reta dentro da reta
Perceba que, dentro de uma reta, pode existir uma semirreta, um segmento de reta, um ponto ou todos eles. Por isso, dizemos que a reta é um “espaço unidimensional”. Assim, na Geometria, a palavra espaço não é usada apenas no sentido convencional, mas para qualquer “lugar” onde possam existir figuras geométricas com o mesmo número de dimensões ou menos.
Plano
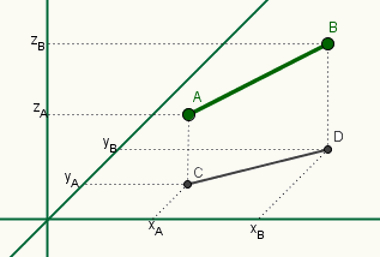
Os planos são conjuntos de pontos formados por uma sequência de retas que não fazem curva. Tomando um plano horizontal como exemplo, sabemos que ele foi formado por infinitas retas. Qualquer reta que tenha sido colocada um pouco acima ou abaixo não faz parte desse plano.

Sobre os planos é possível desenhar figuras que possuem comprimento e largura, por isso, ele é bidimensional. É impossível desenhar qualquer objeto que possua profundidade, a não ser em perspectiva, sobre um plano. A figura a seguir mostra o esquema de uma piscina desenhada sobre o plano.

Perceba que somente a superfície da piscina está em contato com o plano, isto é, somente a parte necessária para medir seu comprimento e sua largura. Sua profundidade (também chamada de altura, a depender da figura geométrica) está toda fora do plano. Para contemplar a profundidade, é necessário definir a terceira dimensão.
Como o plano é bidimensional, infinito e ilimitado, todas as figuras geométricas que possuem duas, uma ou nenhuma dimensão podem ser construídas nele. Assim, o plano é o “espaço bidimensional”.
Espaço
Tendo em vista a imagem anterior, bastaria definir uma terceira dimensão que contemplasse todo o espaço acima e abaixo do plano para que toda a piscina pertencesse a ele. Esse espaço é obtido pelo empilhamento de planos de modo que não haja nenhum espaço entre dois deles, do mesmo modo que o plano é feito de retas e que a reta é feita de pontos.
O espaço é o local onde toda a Geometria conhecida até o Ensino Médio é definida. Todos os sólidos e figuras geométricas são definidos dentro dele.