Existem três posições relativas entre duas retas que se encontram no mesmo plano: as retas podem ser paralelas, coincidentes ou concorrentes. Quaisquer retas que se encontrem em apenas um ponto serão chamadas concorrentes e existem algumas formas de encontrar as coordenadas do ponto de intersecção entre elas.
As retas paralelas, por sua vez, são aquelas que, em toda a sua extensão, não possuem um ponto sequer em comum. Geometricamente, o que se vê são linhas lado a lado.
Finalmente, as retas coincidentes são aquelas que possuem dois pontos em comum. É impossível que, possuindo dois pontos em comum, duas retas não compartilhem todos os seus pontos. Portanto, geometricamente, o que se vê ao olhar duas retas coincidentes é apenas uma reta.
Para encontrar as coordenadas do ponto de intersecção de duas retas concorrentes, será necessário encontrar primeiro as equações dessas duas retas. Após isso, será mais fácil utilizar essas equações em sua forma reduzida.
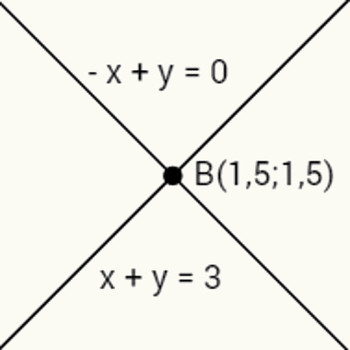
Tomaremos como exemplo as retas presentes na imagem seguinte:

Para descobrir as coordenadas do ponto B, que é o ponto de intersecção entre duas retas concorrentes, utilizaremos a seguinte estratégia:
1 – Tomamos as equações das duas retas e escrevemo-las da forma reduzida.
–x + y = 0
y = x + 0
y = x
–x – y = –2
–y = –2 + x
y = 2 – x
2 – Como as duas equações encontradas são iguais a y, então as duas equações podem ser igualadas. Esse procedimento dará o valor da coordenada x do ponto B.
x = 2 – x
x + x = 2
2x = 2
x = 2
2
x = 1
3 – Para encontrar o valor da coordenada y do ponto B, basta substituir o valor encontrado para x em uma das duas equações reduzidas da reta.
y = 2 – x
y = 2 – 1
y = 1
Portando, as coordenadas do ponto B são: x = 1 e y = 1 e escrevemos B = (1,1) ou B (1,1).
Portanto, para encontrar as coordenadas do ponto de intersecção entre duas retas, devemos resolver o sistema de equações construído a partir das equações dessas duas retas. As imagens não são necessárias para solução de problemas como esse. Elas são indispensáveis para determinar as equações das retas e auxiliam na verificação dos resultados. Contudo, observe que o próximo exemplo foi resolvido sem o uso de qualquer imagem.
Exemplo 2 – Qual a localização do ponto B, que é a intersecção entre as retas –2x + y = 0 e –x – 2y = – 10?
Para resolver, lembre-se: basta montar um sistema de equações utilizando as equações das retas coincidentes:
–2x + y = 0
–x – 2y = – 10
y = 0 + 2x
– 2y = – 10 + x
y = 2x
2y = 10 – x
Agora, é necessário igualar as variáveis. Multiplicaremos a primeira equação por 2.
(2)y = (2)2x
2y = 10 – x
2y = 4x
2y = 10 – x
Agora, sim, estamos aptos a igualar as equações:
2y = 2y, portanto:
4x = 10 – x
4x + x = 10
5x = 10
x = 5
Como no exemplo 1, usaremos a primeira equação do sistema para descobrir o valor de y:
y = 2x
y = 2·5
y = 10
Dessa forma, as coordenadas do ponto B são: x = 5 e y = 10 e escrevemos B = (5,10) ou B (5,10).
Videoaula relacionada: