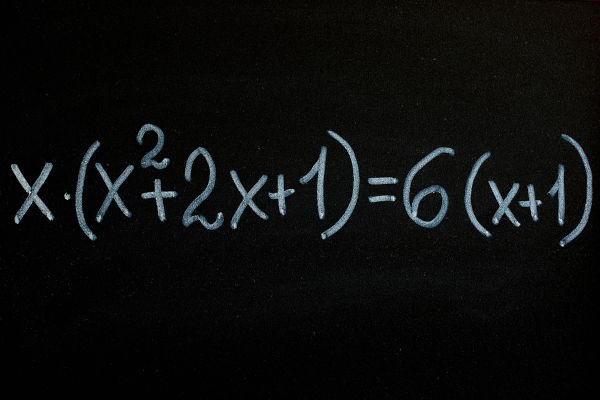Polinômios

Polinômios são expressões algébricas formadas pela soma de monômios distintos, ou seja, que não são semelhantes entre si. Cada monômio é composto por um coeficiente e uma parte literal (variável elevada a um expoente). Quando há termos semelhantes em dois polinômios, é possível simplificar a expressão pela redução de termos durante a adição ou a subtração. A multiplicação entre polinômios é feita utilizando a propriedade distributiva, já a divisão pode ser realizada pelo método de chaves. O grau do polinômio é determinado pelo grau do maior monômio.

Leia também: Afinal, o que são monômios?

Tópicos deste artigo

• 1 - Resumo sobre polinômios
• 2 - O que são polinômios?
• 3 - Monômio, binômio e trinômio
• 4 - Grau dos polinômios
• 5 - Operações com polinômios
  • → Adição e subtração de polinômios
  • → Multiplicação de polinômios
  • → Divisão de polinômios
• 6 - Fatoração de polinômios
• 7 - Exercícios resolvidos sobre polinômios

Resumo sobre polinômios

• Polinômios são expressões algébricas formadas pela soma de monômios distintos.
• São classificados, de acordo com o número de termos, como monômios, binômios e trinômios.
• O grau do polinômio é igual ao grau do maior monômio.
• Utilizamos polinômios para representar variáveis, como em funções e em fórmulas.
• As operações com polinômios envolvem operações básicas, como adição, subtração, multiplicação e divisão.
• A fatoração de polinômios é uma técnica para simplificar expressões algébricas.

O que são polinômios?

Polinômios são expressões algébricas compostas pela soma de vários termos, em que cada termo é formado por um número, conhecido como coeficiente, multiplicado por uma variável elevada a um expoente natural. Um polinômio pode ter um ou mais termos. Exemplos:

• 3x² + 2x - 5
• x³- 4x² + 7xy³
• 2ab²+3a²b - 5

Monômio, binômio e trinômio

O polinômio recebe nome especial de acordo com o número de termos que ele tem.

• Monômio: expressão algébrica com apenas um termo, como 4x².
• Binômio: polinômio com dois termos, como 3x + 8.
• Trinômio: polinômio com três termos, como 2x² + 4x - 3.

Veja também: Expressões algébricas — como resolver expressões que têm letras e números

Grau dos polinômios

O grau de um polinômio é o maior expoente da variável presente entre os termos do polinômio. O grau é uma característica fundamental, pois indica a potência da variável que tem o maior impacto no comportamento do polinômio, especialmente quando se estuda o gráfico dessa variável. Para determinar o grau de um polinômio, identifica-se o maior expoente da variável (ou das variáveis) em cada termo, e o grau do polinômio será o maior desses expoentes.

• Exemplo 1:

Consideremos o polinômio:

P(x) = 5x³ - 2x² + 7x - 4

Aqui, temos quatro termos:

• 5x³: o expoente da variável x é 3.
• -2x²: o expoente da variável x é 2.
• 7x: o expoente da variável x é 1.
• -4: termo constante.

O maior expoente é 3, logo, o grau desse polinômio é 3. Dizemos que é um polinômio de terceiro grau.

• Exemplo 2:

Consideremos o polinômio:

Q(x) = 3x⁴ + 6x³ - x² + 9

Aqui, temos quatro termos:

• 3x⁴: o expoente da variável x é 4.
• 6x³: o expoente da variável x é 3.
• -x²: o expoente da variável x é 2.
• 9: termo constante.

O maior expoente é 4, logo, o grau desse polinômio é 4. Dizemos que é um polinômio de quarto grau.

Operações com polinômios

As operações básicas com polinômios envolvem adição, subtração, multiplicação e divisão. Cada uma delas segue regras específicas:

→ Adição e subtração de polinômios

Para adicionar ou subtrair polinômios, somamos ou subtraímos os coeficientes dos termos que têm a mesma parte literal, ou seja, mesma variável e mesmo expoente.

Exemplo:

(5x² + 5x – 2) + (2x² – 4x + 3) = 7x² + x + 1

(2x³ – 2x + 1) – (x³ + x – 4) = x³ - 3x + 5

→ Multiplicação de polinômios

Ao multiplicar polinômios, utiliza-se a propriedade distributiva, multiplicando cada termo do primeiro polinômio por cada um dos termos do segundo polinômio.

Exemplo:

(x+2) ⋅ (x - 3) = x² - 3x + 2x - 6 = x² - x – 6

(2x² + 3x – 2) ⋅ (x²–1) = 2x⁴ - 2x² + 3x³ - 3x - 2x² + 2 = 2x⁴ + 3x³ - 4x²+2

• Videoaula sobre adição, subtração e multiplicação de polinômios

→ Divisão de polinômios

A divisão de polinômios é feita como a divisão euclidiana.

Exemplo:

 (15x² + 11x + 2) : (3x + 1)

Primeiro vamos armar a conta utilizando o método de chaves:

Agora, vamos dividir o primeiro termo do dividendo pelo primeiro termo do divisor, 15x² : 3x = 5x. O valor encontrado vai para o quociente, logo, temos que:

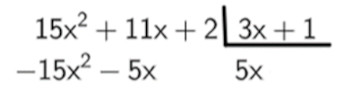
Note que 5x foi multiplicado por 3x e por 1 e o resultado foi colocado abaixo do dividendo com o seu sinal foi invertido. Agora, realizando a subtração, encontramos um novo polinômio:

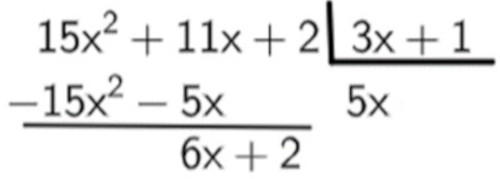
Vamos repetir o processo. Sabemos que 6x : 3x = 2, logo, temos que:

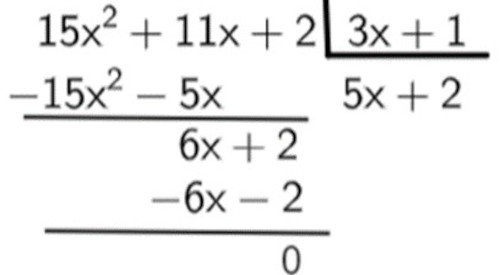
Assim, o resultado da divisão entre 15x² + 11x + 2 e 3x + 1 é o polinômio 5x + 2.

• Videoaula sobre adição, subtração e multiplicação de polinômios

Fatoração de polinômios

A fatoração de polinômios é o ato de reescrever um polinômio como o produto de dois ou mais polinômios de grau menor. Utilizamos a fatoração para simplificar expressões envolvendo polinômios.

• Fatoração por fator comum: quando todos os termos de um polinômio têm um fator comum. Exemplo:

2x² + 4x = 2x (x + 2)

• Trinômio quadrado perfeito: quando um polinômio pode ser escrito como o quadrado de um binômio. Exemplo:

x² + 6x + 9 = (x + 3)²

• Diferença de dois quadrados: quando um polinômio é uma diferença entre dois quadrados. Exemplo:

x² – 9 = (x – 3) (x + 3)

Saiba mais: Como se calcula o MMC de polinômios?

Exercícios resolvidos sobre polinômios

(Enem) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).

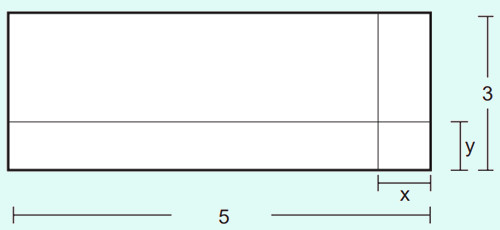
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:

A) 2xy

B) 15 − 3x

C) 15 − 5y

D) -5y − 3x

E) 5y + 3x − xy

Resolução:

Alternativa E

Para calcular a área perdida, primeiro sabemos que a área anterior era de 3 ⋅ 5 = 15; entretanto, a área depois de lavar foi de:

(5 – x) (3 – y) = 15 – 5y – 3x + xy

Então a área total será de:

15 - (15 - 5y - 3x + xy)

15 - 15 + 5y + 3x - xy

5y + 3x – xy

Questão 2

Dado os polinômios P(x) = 4x⁴ - 4x³ + x - 1 e D(x) = 4x³ + 1, o quociente da divisão entre eles é igual a:

A) x – 1

B) x + 1

C) x + 2

D) 0

E) 1

Resolução:

Alternativa A

Calculando a divisão, temos que:

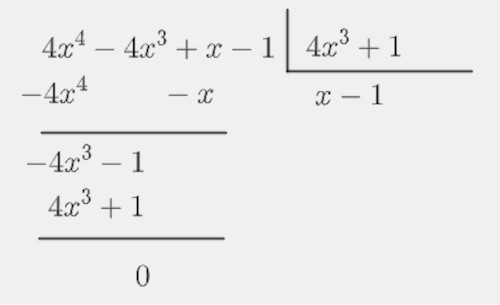
Fonte

MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.