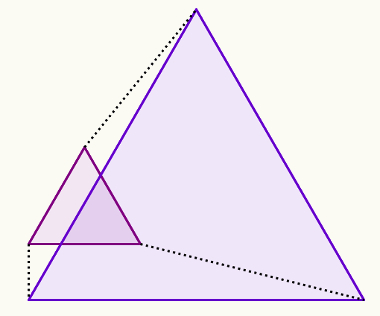
As conclusões mais comuns de uma pessoa que compara duas figuras são: que essas figuras são iguais, que essas figuras são parecidas ou que essas figuras são diferentes.
Em Geometria, as figuras comparadas podem ser congruentes, semelhantes ou diferentes. Figuras congruentes são aquelas que possuem as mesmas características e o mesmo tamanho; figuras semelhantes são aquelas que possuem as mesmas características, mas tamanhos diferentes; já as figuras diferentes são aquelas que sequer possuem características parecidas.
Com relação aos polígonos, essas características a que nos referimos são os ângulos e os lados. Para que dois polígonos sejam congruentes, é necessário que as medidas de seus ângulos e lados correspondentes sejam congruentes.

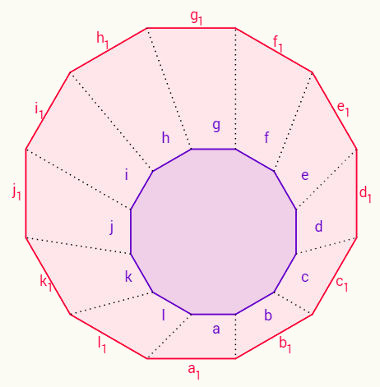
Os dodecágonos acima são regulares e, por isso, possuem todos os lados e ângulos iguais. Comparando os dois, observamos que os lados e os ângulos correspondentes são congruentes e, por isso, os dois polígonos são congruentes.
Para que dois polígonos sejam semelhantes, é necessário que as medidas de seus ângulos sejam congruentes e as medidas de seus lados correspondentes sejam proporcionais.

Observe agora que os polígonos acima, apesar de terem o mesmo formato, não possuem o mesmo tamanho. Isso se dá porque esses dodecágonos regulares possuem ângulos correspondentes congruentes (repare que isso significa que os ângulos do primeiro polígono possuem as mesmas medidas dos ângulos do segundo polígono) e lados correspondentes proporcionais, isto é, se dividirmos os valores dos lados do primeiro polígono pelos lados correspondentes a eles no segundo polígono, o resultado sempre será o mesmo, no caso, 2.
Portanto, para que dois polígonos sejam semelhantes, eles devem cumprir os três requisitos seguintes:
1 – Possuir o mesmo número de lados;
2 – Possuir ângulos internos respectivos congruentes;
3 – Possuir lados correspondentes proporcionais.
Propriedades
A respeito dos polígonos que se enquadram nesses requisitos, existem duas propriedades básicas:
Propriedade 1 – Dois polígonos congruentes são também semelhantes. Se dois polígonos são congruentes, eles já possuem o mesmo número de lados, além de possuírem ângulos internos respectivos congruentes e lados correspondentes congruentes. Como os lados são correspondentes, a divisão entre eles sempre dará 1, independentemente do tamanho dos lados. Portanto, esses lados são proporcionais, o que classifica os polígonos como semelhantes.
Propriedade 2 – Dois polígonos semelhantes possuem perímetros e diagonais proporcionais às medidas de dois lados correspondentes. Observe essa propriedade no exemplo seguinte:

Esses polígonos são regulares (foram construídos assim) e, por isso, possuem todos os lados e ângulos iguais. Comparando os dois, teremos o mesmo número de lados, ângulos respectivos congruentes e lados correspondentes congruentes. Dessa forma, eles são semelhantes. A propriedade 2 garante que os perímetros desses polígonos são proporcionais a dois lados quaisquer.
Para verificar essa propriedade, observe que a base do primeiro polígono é 2 e a base do segundo é 1. Os perímetros desses polígonos, respectivamente, são: 24 e 12. Agora escreva as razões respeitando a ordem do primeiro polígono para o segundo:
2 = 24 = 2
1 12
Videoaula relacionada: