Um polígono é considerado convexo quando não possui reentrâncias, ou seja, quando nenhum de seus vértices aponta para o interior dessa figura. Na imagem a seguir, por exemplo, o polígono ABCDE não apresenta nenhuma reentrância. Diferentemente, o polígono FGHIJ possui reentrância no vértice H.
O polígono ABCDE é chamado convexo, e o polígono FGHIJ é denominado não convexo.
Definição formal
Embora possa ser usada para reconhecer polígonos convexos, a definição acima não é formalmente usada na Geometria. A definição de polígonos convexos, portanto, é:
Se em um dado polígono c com dois pontos quaisquer A e B dentro dele, não existir nenhuma posição em que pelo menos um dos pontos do segmento AB não pertença à parte interna do polígono c, então, esse polígono é convexo.
Em outras palavras, qualquer segmento cujas extremidades são pontos interiores de um polígono convexo tem que estar totalmente inserido nesse polígono também.
A imagem abaixo mostra um exemplo de segmento AB, à esquerda, dentro de um polígono convexo. À direita, existe uma possibilidade de escolher a posição do segmento AB que faz com que uma parte dele não esteja dentro do polígono. Nesse caso, esse não é um polígono convexo.

Elementos de um polígono convexo
Os elementos de um polígono convexo são:
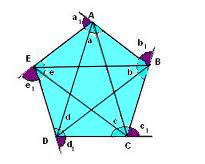
1 – Lados: são os segmentos de reta que limitam o polígono. No exemplo a seguir, o segmento AB é um lado.
2 – Vértices: são os pontos de encontro entre dois lados. São representados na seguinte imagem por letras maiúsculas.
3 – Diagonais: são os segmentos de reta que ligam dois vértices não consecutivos de um polígono convexo, como o segmento AD na figura a seguir.
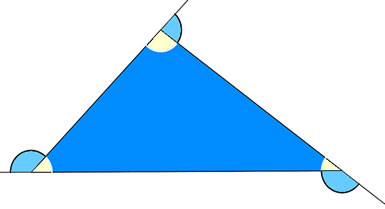
4 – Ângulos internos: cada ângulo entre dois lados consecutivos de um polígono voltado para seu interior é um ângulo interno. Como exemplo, temos o ângulo EDC na figura a seguir.
5 – Ângulos externos: cada ângulo entre um lado e o prolongamento do lado consecutivo a ele no exterior do polígono é um ângulo externo. O ângulo CDK, presente na figura a seguir, é um exemplo de ângulo externo.
Propriedades de um polígono convexo
1ª – Em um polígono convexo, o número de lados é sempre igual ao número de ângulos internos e vértices.
2ª – É possível encontrar a soma dos ângulos internos de um polígono convexo usando a seguinte fórmula:
S = (n – 2)180
Na qual S é a soma dos ângulos internos do polígono e n é o número de lados que ele possui.
3ª – Todo polígono apresenta a soma de seus ângulos externos igual a 360°.
4ª – O número de diagonais que um polígono convexo possui é obtido pela seguinte fórmula:
d = n(n – 3)
2
Em que d é o número de diagonais do polígono e n é o seu número de lados.
Exemplo: Dado um hexágono convexo, calcule:
a) A soma de seus ângulos internos.
S = (n – 2)180
S = (6 – 2)180
S = (4)180
S = 720°
b) O número de diagonais desse hexágono.
d = n(n – 3)
2
d = 6(6 – 3)
2
d = 6(3)
2
d = 18
2
d = 9 diagonais.
Aproveite para conferir nossas videoaulas sobre o assunto: