Os poliedros são formas geométricas bastante comuns no nosso cotidiano. Caixas, cubos, prédios, pirâmides — todos são exemplos de poliedros presentes no nosso dia a dia. Para que um sólido geométrico seja classificado como um poliedro, é necessário que ele possua faces formadas por polígonos e que seja fechado. Quando todas as arestas e ângulos internos são iguais, esses poliedros são conhecidos como poliedros regulares.
Um poliedro também pode ser classificado como convexo ou côncavo. Quando o poliedro é convexo, é possível utilizar a relação de Euler, que torna possível calcular a quantidade de vértices, arestas ou faces por meio da fórmula V + F = A + 2.
Os principais poliedros são os prismas e as pirâmides. Existem também os sólidos de Platão: o tetraedro, hexaedro, octaedro, dodecaedro e icosaedro, que são inclusive os únicos poliedros regulares convexos.
Leia também: Principais diferenças entre figuras planas e espaciais
Tópicos deste artigo
- 1 - Resumo sobre poliedros
- 2 - Videoaula sobre poliedros
- 3 - Elementos de um poliedro
- 4 - Poliedros convexos e não convexos (côncavos)
- 5 - Poliedros regulares ou sólidos de Platão
- 6 - Prismas
- 7 - Pirâmide
- 8 - Relação de Euler
- 9 - Exercícios resolvidos sobre poliedros
Resumo sobre poliedros
-
Poliedros são sólidos geométricos formados por faces poligonais, com face, aresta e vértice.
-
Um poliedro pode ser convexo ou côncavo.
-
Os principais poliedros convexos são os prismas e as pirâmides.
-
Existem os chamados sólidos de Platão, que são poliedros regulares e convexos. São eles:
-
tetraedro;
-
hexaedro ou cubo;
-
octaedro;
-
icosaedro;
-
dodecaedro.
-
-
Em poliedros convexos, há uma relação entre o número de vértices, faces e arestas, conhecida como relação de Euler:
-
V + F = A + 2
-
Videoaula sobre poliedros
Elementos de um poliedro
Chamamos de poliedro qualquer sólido geométrico que possui suas faces formadas por polígonos. Podemos citar como exemplo o cubo, que possui todas as suas faces constituídas por quadrados, ou a pirâmide, que pode possuir a base formada por um polígono qualquer e faces laterais formadas por triângulos, entre vários outros casos presentes em nosso mundo.
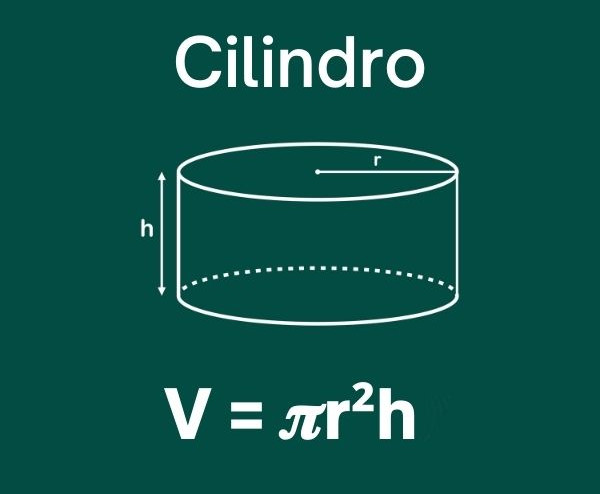
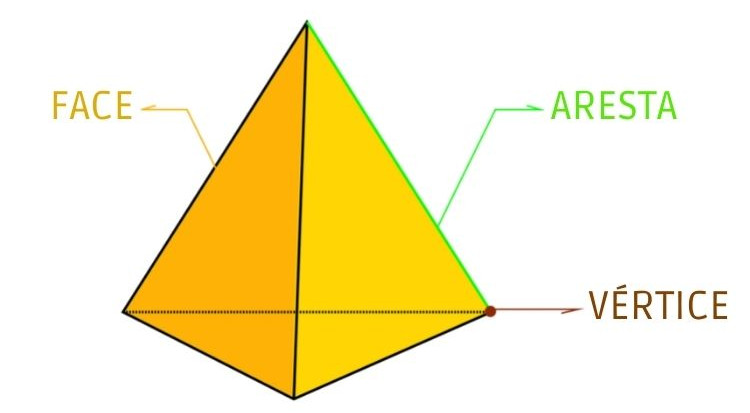
Não são poliedros sólidos geométricos que possuem forma arredondada, como o cilindro, o cone e a esfera. Em um poliedro, os principais elementos são os vértices, as arestas e as faces.
Poliedros convexos e não convexos (côncavos)
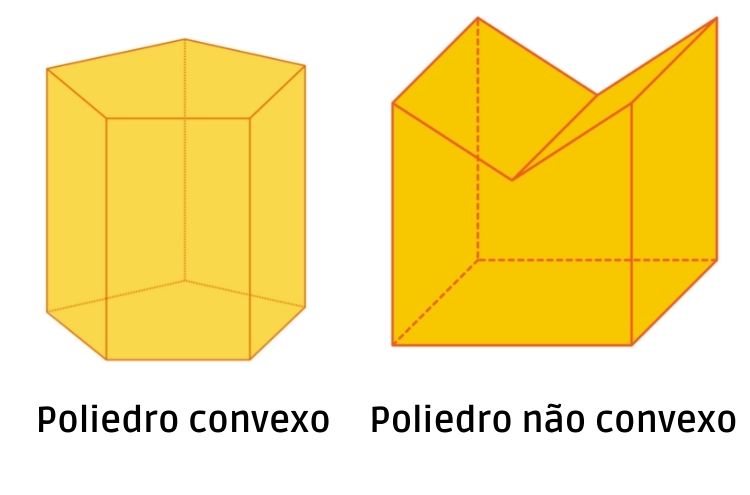
Quando analisamos os poliedros, podemos classificá-los como convexos ou não convexos (côncavos). Quando qualquer segmento de reta que liga dois pontos contidos no poliedro está inserido totalmente dentro do poliedro, então este será convexo. Caso contrário, ele será côncavo, ou seja, não convexo.
Poliedros regulares ou sólidos de Platão
Um poliedro pode ser classificado como regular quando todas as suas faces são o mesmo polígono e suas arestas são todas congruentes. Existem cinco poliedros que são regulares e convexos:
-
tetraedro;
-
hexaedro (cubo);
-
octaedro;
-
icosaedro;
-
dodecaedro.
Os poliedros regulares também são conhecidos como sólidos de Platão, pelo fato de eles terem sido objeto de estudo desse pensador.
-
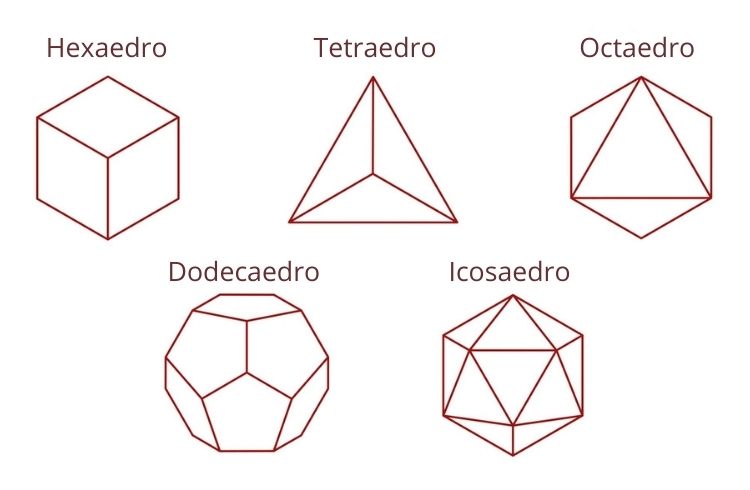
Tetraedro: é o sólido geométrico que possui 4 faces, todas triangulares e congruentes, e também 4 vértices e 6 arestas. Ele é um caso particular de pirâmide, que possui todas as faces triangulares.
-
Hexaedro: é o sólido geométrico que possui 6 faces no formato de quadrados, 8 vértices e 12 arestas. O hexaedro é conhecido também como cubo.
-
Octaedro: é o sólido geométrico que possui 8 faces triangulares, 6 vértices e 12 arestas.
-
Dodecaedro: é o sólido geométrico que possui 12 faces pentagonais, 20 vértices e 30 arestas.
-
Icosaedro: é o sólido geométrico que possui 20 faces triangulares, 12 vértices e 30 arestas.
Leia também: Geometria espacial no Enem — como esse tema é cobrado?
Prismas
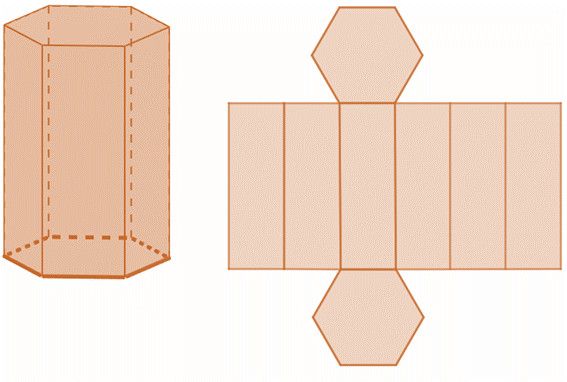
Além dos poliedros regulares, existem outros dois grandes grupos de sólidos. O primeiro deles é o de prismas, que são sólidos geométricos com duas bases formadas por polígonos quaisquer e faces laterais formadas por paralelogramos.
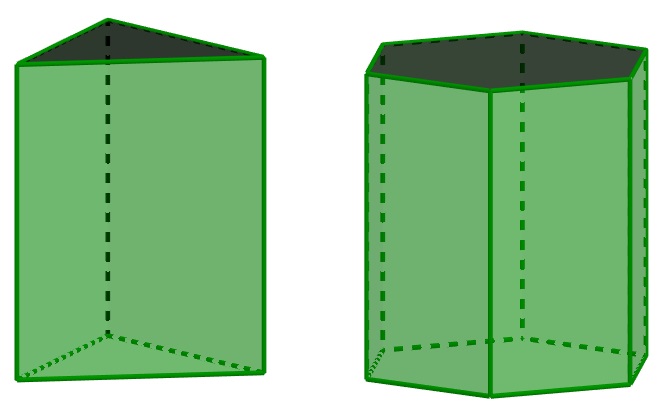
Existem vários outros tipos de prisma, a depender diretamente do polígono que forma as suas bases. Para saber mais sobre esse poliedro, leia: Prisma.
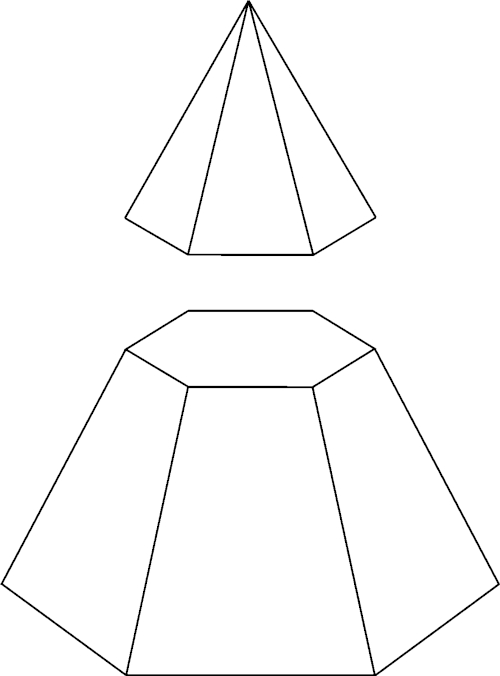
Pirâmide
Outro grande grupo de poliedros é o das pirâmides. A pirâmide possui uma base formada por qualquer polígono, e os vértices desse polígono são ligados a um ponto conhecido como vértice da pirâmide, formando áreas laterais triangulares. Para conhecer esse poliedro, leia: Pirâmide.
Relação de Euler
A relação de Euler é uma fórmula que relaciona o número de vértices, faces e arestas em poliedros convexos. Euler percebeu que a quantidade de elementos que um poliedro tem se relaciona pela fórmula:
|
V + F = A + 2 |
Exemplo:
Qual é o número de faces de um poliedro que possui 20 vértices e 30 arestas?
Resolução:
Temos que V = 20 e A = 30.
Substituindo, na fórmula de Euler:
V + F = A + 2
20 + F = 30 + 2
20 + F = 32
F = 32 – 20
F = 12
Leia também: Paralelepípedos — sólidos tridimensionais cujas faces são paralelogramos
Exercícios resolvidos sobre poliedros
Questão 1
Julgue as afirmativas a seguir:
I → O cilindro é um prisma de base circular.
II → O cubo é um poliedro regular.
III → O cone é um caso particular de pirâmide.
Marque a alternativa correta.
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Resolução:
Alternativa B
I → A base de um prisma deve ser um polígono. O círculo não se configura como um polígono, logo o cilindro não é um prisma. (Falsa)
II → (Verdadeira)
III → A base de uma pirâmide deve ser um polígono, e o círculo, base do cone, não é um polígono. Portanto, o cone não é uma pirâmide. (Falsa)
Questão 2
Os sólidos de Platão são conhecidos como os únicos poliedros regulares, ou seja, todas as suas faces são iguais. Os poliedros a seguir são considerados sólidos de Platão, exceto o:
A) cubo.
B) dodecaedro.
C) tetraedro.
D) paralelepípedo.
E) icosaedro.
Resolução:
Alternativa D
Da lista, o único que não é um sólido de Platão é o paralelepípedo.