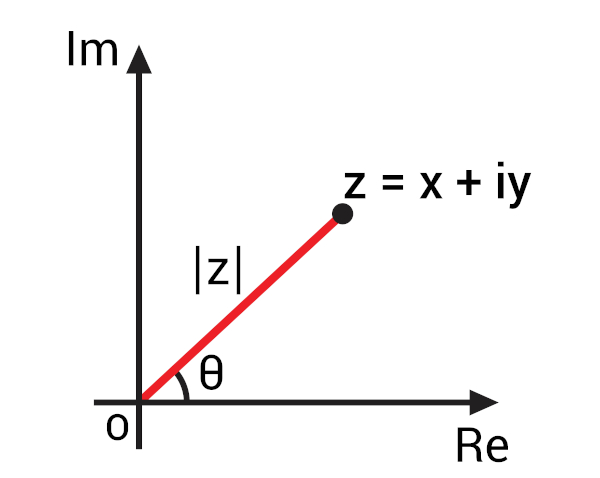
O plano de Argand-Gauss é utilizado para representar geometricamente os números complexos. Com as contribuições dos matemáticos Argand e Gauss, foi possível fazer um estudo mais aprofundado desses números, como o cálculo do módulo e do argumento de um número complexo.
Esse plano é também conhecido como plano complexo, pois, dado um número complexo da fórmula algébrica z = x + yi, em que x é a parte real e y é a parte imaginária, ele será representado no plano complexo como o ponto Z (x,y). A representação de um número complexo no plano de Argand-Gauss recebe o nome de afixo ou imagem geométrica do número z.
Leia também: Como calcular as potências de i?
Tópicos deste artigo
- 1 - Representação geométrica de números complexos
- 2 - Afixos
- 3 - Número complexo
- 4 - Imaginário puro
- 5 - Número real
- 6 - Módulo de um número complexo
- 7 - Argumento de um número complexo
- 8 - Exercícios resolvidos
Representação geométrica de números complexos
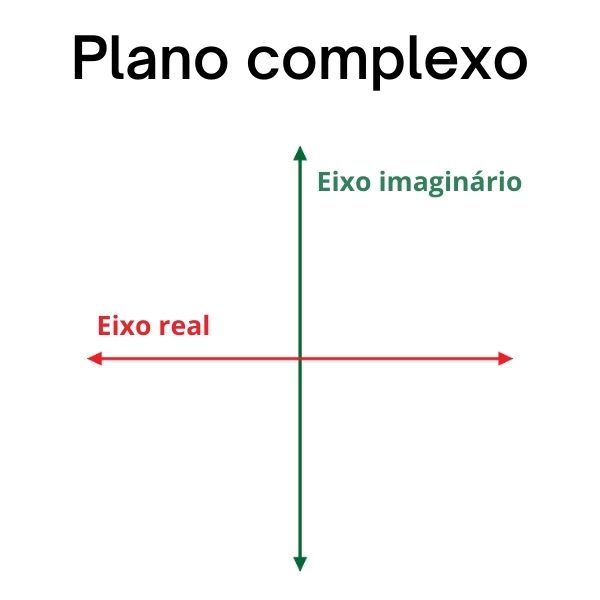
Conhecemos como plano de Argand-Gauss, ou plano complexo, o plano formado por dois eixos perpendiculares, que utilizamos para fazer a representação geométrica de um número complexo e, consequentemente, desenvolver conceitos importantes para esses números, como a análise na geometria analítica, o desenvolvimento da fórmula trigonométrica de números complexos e o estudo do argumento e do módulo.
Os números complexos foram estudados na tentativa de resolver equações com raiz quadrada de um número negativo. Os matemáticos desenvolveram os estudos dos números complexos chamando de i a √-1, representando-os de forma algébrica da seguinte forma: z = x + yi.
Para representar um número complexo no plano de Argand-Gauss, foi definido que o eixo horizontal é o eixo da parte real de um número complexo, e o eixo vertical é o eixo da parte imaginária, logo o número complexo z = x + yi é representado pelo ponto (x,y).
Afixos
Os pontos que representam os números complexos no plano de Argand-Gauss recebem o nome de afixos ou imagem do número complexo z. Na representação desses afixos, existem três possibilidades:
-
o número complexo pode ser um número real, quando a sua parte imaginária é igual a zero;
-
o número complexo pode ser um imaginário puro, quando a sua parte real é igual a zero;
-
por fim, ele pode ser um número complexo qualquer, quando a sua parte real e a sua parte imaginária são diferentes de zero.
Veja também: Operações com números complexos na forma algébrica
Número complexo
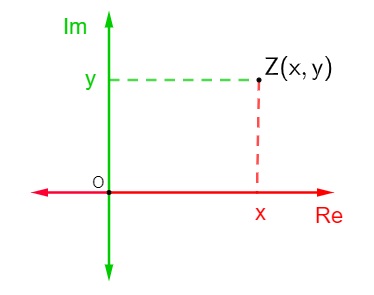
A representação de um número complexo z = x + yi no plano complexo é bastante simples. Cada um dos eixos é composto por números reais, então basta encontrar a posição do ponto Z (x,y) no plano de Argand-Gauss para representar esse ponto.
Supondo que esse número complexo não seja nem imaginário puro e nem um número real, ou seja, x e y são diferentes de 0, então o ponto Z será um ponto que está em um dos quadrantes do plano complexo.
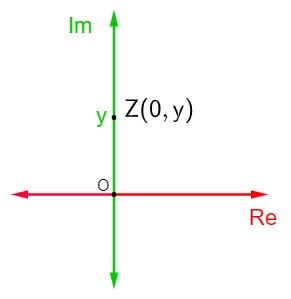
Imaginário puro
Um número complexo é conhecido como imaginário puro, quando a sua parte real é igual a zero, ou seja, z = yi. Quando isso acontece, ao representar esse número imaginário puro no plano de Argand-Gauss, esse ponto vai ser um ponto do tipo Z(0,y). Esse ponto pertence ao eixo vertical, ou seja, o número complexo imaginário puro pertence ao eixo da parte imaginária do plano, o que faz todo sentido, já que esse número não possui parte real.
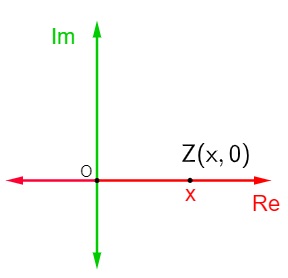
Número real
Utilizando um raciocínio análogo ao do imaginário puro, quando um número complexo é também um número real, significa que a sua parte imaginária é igual a zero, então esse número possui representação algébrica z = x. Como a sua parte imaginária é igual a zero, ele é representado pelo ponto Z(x,0). Números complexos que possuem parte imaginária nula são representados por pontos em cima do eixo da parte real.
Exemplos:
Agora vejamos a representação de alguns números complexos no plano de Argand-Gauss.
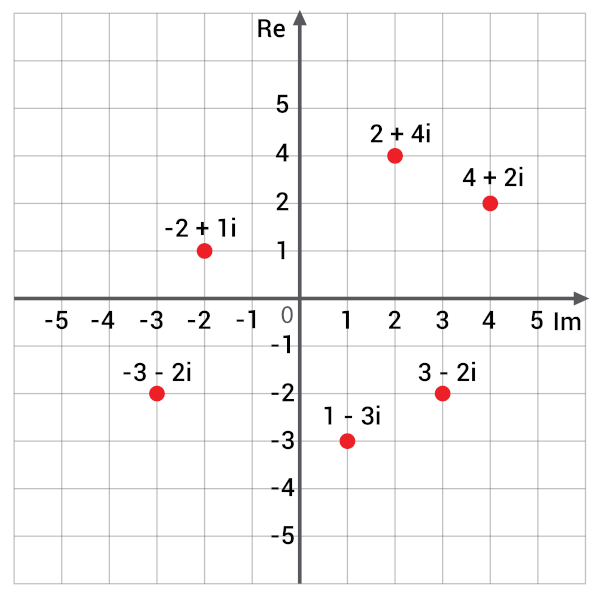
Módulo de um número complexo
Compreendendo a representação de um número complexo no plano complexo, é possível desenvolver o conceito de módulo para um número complexo. Quando estudamos o conjunto dos números reais, aprendemos que módulo nada mais é do que a distância que um número tem até o 0.
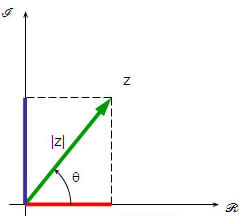
Estendendo a ideia de módulo a um número complexo, o módulo também é a distância que um número complexo tem do número real 0, porém, como estamos trabalhando com um número composto por parte real e parte imaginária, para calcular o módulo de um número complexo, vamos encontrar a distância do ponto Z(x,y) até o ponto O (0,0).
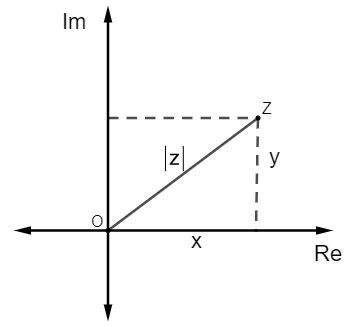
Note que |z| nada mais é do que a hipotenusa do triângulo, o que torna possível calcular o módulo utilizando o teorema de Pitágoras.
|z|² = x² + y²
Exemplo:
Calcule o módulo do número complexo z = 3 + 4i.
|z|² = 3² + 4²
|z|² = 9 + 16
|z|² = 25
|z| = √25
|z| = 5
Veja também: Função modular – função cuja variável se encontra dentro do módulo
Argumento de um número complexo
Conhecemos como argumento de um número complexo o ângulo que o vetor OZ forma com o eixo horizontal no plano cartesiano.
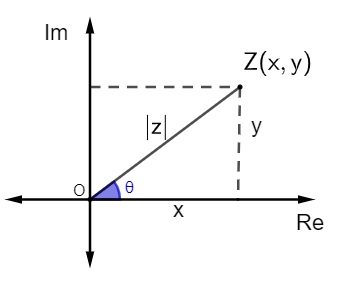
Para encontrar o valor do ângulo, utilizamos as razões trigonométricas seno e cosseno.
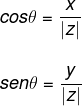
Encontrando o valor do seno e do cosseno, vamos procurar o ângulo θ que possui como argumento os valores encontrados.
Exemplo:
Calcule o argumento do número complexo z = 1 + i.
Primeiro vamos calcular o valor do |z|:
|z|² = 1² + 1²
|z|² = 1 + 1
|z|² = 2
|z| = √2
Agora que conhecemos o valor de |z|, temos que:
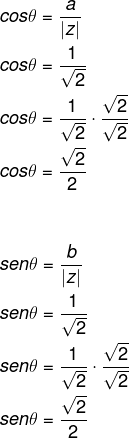
Sabemos que o ângulo que possui os valores para seno e cosseno iguais aos valores encontrados é o ângulo de 45º. Podemos representá-lo em graus ou radianos. Então, o argumento desse número complexo é igual a:
![]()
Exercícios resolvidos
Questão 1 – Na imagem a seguir, estão representados alguns números complexos:
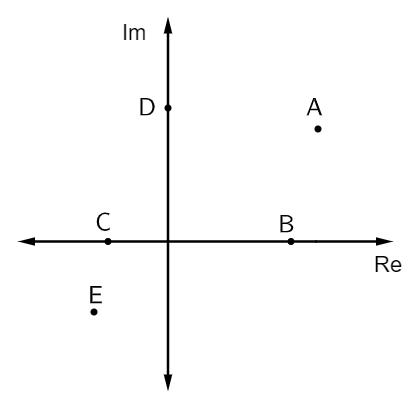
Os afixos de números imaginários puros são:
A) somente C.
B) somente D.
C) somente C e B.
D) somente A e E.
E) somente B, C e D.
Resolução
Alternativa B. Os afixos que são imaginários puros estão em cima do eixo imaginário. No caso, há somente um ponto que pertence a esse eixo, que é o ponto D.
Questão 2 – No plano complexo a seguir, o ponto que representa o número complexo z = 2 – i é:
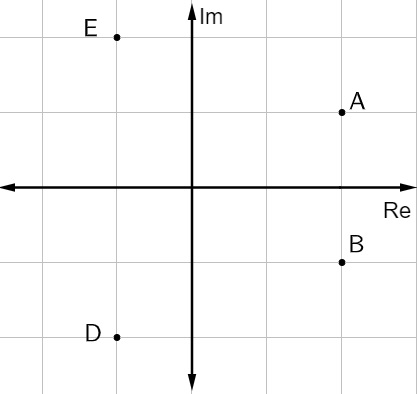
A) A.
B) B.
C) C.
D) D.
E) E.
Resolução
Alternativa B. Analisando a imagem, o ponto que possui parte real igual a 2 e parte imaginária igual a – 1 é o ponto B (2, – 1).