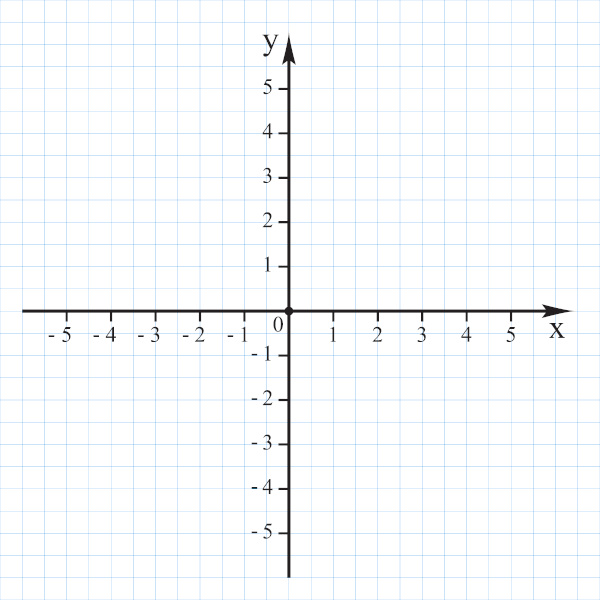
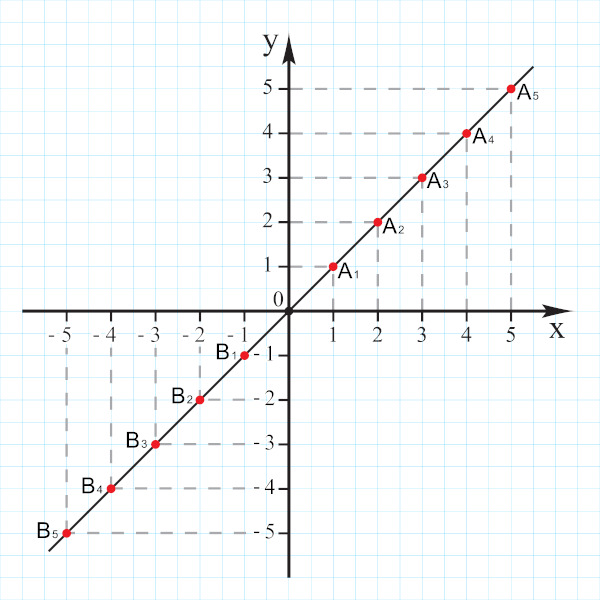
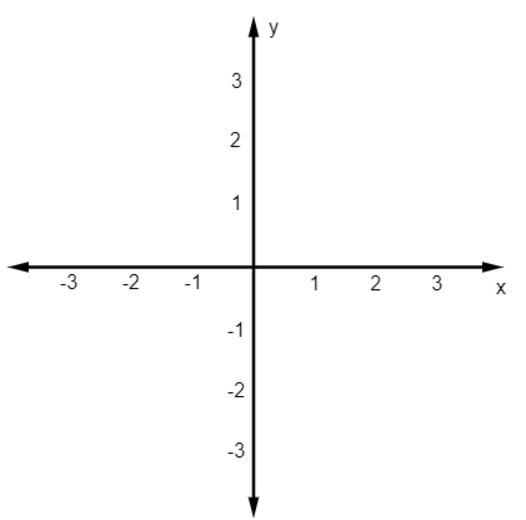
O plano cartesiano, também conhecido como eixo cartesiano, recebe esse nome em homenagem ao matemático René Descartes, que fez várias contribuições para a matemática. O plano cartesiano é formado por duas retas reais, conhecidas também como retas enumeradas. Essas retas são perpendiculares entre si, uma na horizontal, conhecida como eixo das abscissas ou eixo x, e outra na vertical, conhecida como eixo das ordenadas ou eixo y.
O plano cartesiano nos permite inicialmente encontrar a localização de pontos no plano, o par ordenado (x, y) é a representação de um ponto no plano cartesiano, e, com base nesse princípio básico, surgiram vários outros. Estudos foram desenvolvidos com base no plano cartesiano, como a geometria analítica, que envolve a representação de objetos geométricos, como a reta, a circunferência, entre outros.
Leia também: Ponto, reta, plano e espaço – conceitos básicos da geometria
Tópicos deste artigo
- 1 - Resumo sobre o plano cartesiano
- 2 - Videoaula sobre plano cartesiano
- 3 - Como fazer o plano cartesiano?
- 4 - Representação de pontos no plano cartesiano
- 5 - Elementos do plano cartesiano
- 6 - Sinais no quadrante
- 7 - Exercícios resolvidos sobre plano cartesiano
Resumo sobre o plano cartesiano
-
O plano cartesiano é formado por duas retas reais perpendiculares entre si e conhecidas como eixos.
-
O eixo horizontal é conhecido como eixo x.
-
O eixo vertical é conhecido como eixo y.
-
O plano cartesiano é dividido em quatro quadrantes.
-
Todo par ordenado (x, y) pode ser representado por um ponto no plano cartesiano.
Videoaula sobre plano cartesiano
Como fazer o plano cartesiano?
Para construir o plano cartesiano, desenhamos duas retas numeradas e perpendiculares entre si, uma na horizontal, conhecida como eixo x ou eixo das abcissas, e outra na vertical, conhecida como eixo y ou eixo das ordenadas.
Veja mais: Plano de Argand-Gauss – usado para a representação geométrica dos números complexos
Representação de pontos no plano cartesiano
Com a construção do plano cartesiano, é possível representar a localização de pontos no plano. Sabemos que os eixos x e y são numerados, então, podemos representar pontos por meio de um par ordenado (x, y), ordenado porque a ordem é importante, pois, primeiro, sempre teremos o valor da abcissa e, depois, o valor da ordenada.
Exemplo:
Vejamos no plano cartesiano a representação do ponto (3, 2).
Note que a abcissa vale 3, então, encontraremos esse valor no eixo horizontal, e vamos traçar uma reta pontilhada, paralela ao eixo vertical, passando por 3:
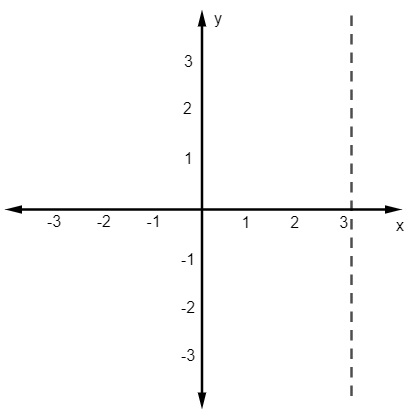
Note que a ordenada vale 2, também encontraremos esse valor no eixo vertical, e traçamos uma reta paralela à reta horizontal, passando por 2.
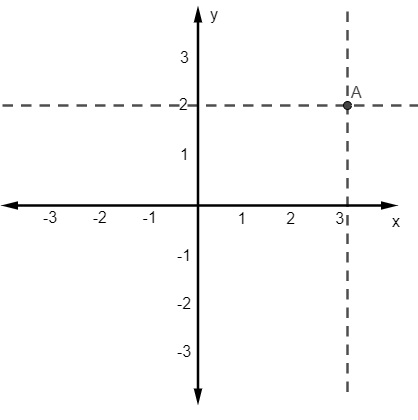
Para representar pontos, geralmente utilizamos letras maiúsculas, assim, o ponto (3, 2) está representado por A no plano cartesiano, que é o encontro das retas pontilhadas. De forma mais organizada, podemos representar esse ponto, eliminando parte das retas tracejadas, da seguinte maneira:
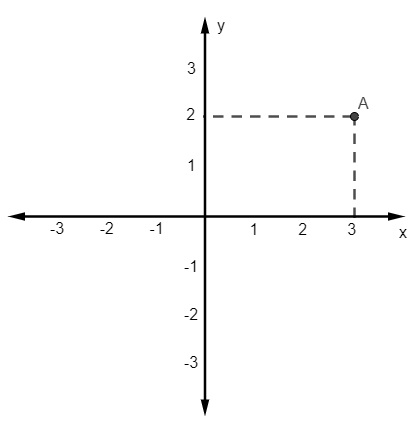
Veja também: O que é o ponto médio de um segmento no plano?
Elementos do plano cartesiano
Quanto construímos o plano cartesiano, ele possui elementos importantes. O encontro dos dois eixos é conhecido como origem, representada pela letra O, e possui coordenadas (0, 0).
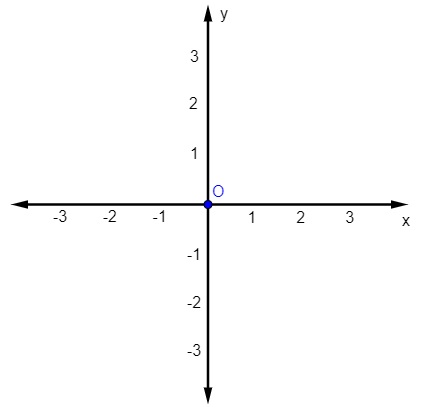
Além da origem, o plano cartesiano é dividido em quatro partes, que conhecemos como quadrantes. Os quadrantes são nomeados no sentido anti-horário, iniciando pelo quadrante que possui valores positivos para as abscissas e ordenadas:
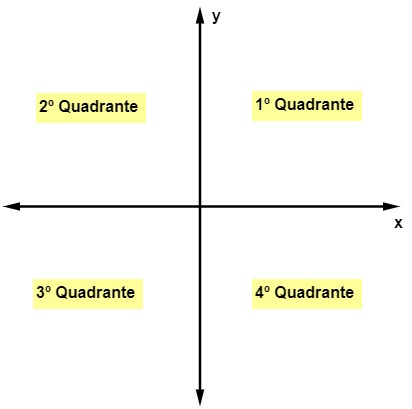
Os quadrantes do plano cartesiano podem ser representados também pela letra maiúscula Q seguida da numeração do quadrante:
-
QI → 1º quadrante
-
QII → 2º quadrante
-
QIII → 3º quadrante
-
QIV → 4º quadrante
Sinais no quadrante
Quando fazemos a representação de pontos no plano cartesiano, fazemos uma análise do sinal do par ordenado para identificar em qual quadrante esse ponto se encontra.

Então, temos que:
1º quadrante, os valores de x e de y são positivos → (+, +)
2º quadrante, o valor de x é negativo e o de y é positivo → (–, +)
3º quadrante, os valores de x e de y são negativos → (– , –)
4º quadrante, o valor de x é positivo e o de y é negativo → (+, –)
Veja também: Quais são as operações básicas envolvendo vetores?
Exercícios resolvidos sobre plano cartesiano
Questão 1 - Sobre o plano cartesiano, julgue as afirmativas a seguir:
I - O eixo vertical é conhecido também como eixo das ordenadas.
II - O ponto A (5, -3) é um ponto do terceiro quadrante.
III - O eixo horizontal é conhecido também como eixo das coordenadas.
Podemos afirmar que:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas II e III são verdadeiras.
E) Somente as afirmativas I e III são verdadeiras.
Resolução
Alternativa A
I → Verdadeira
II → Falsa. As coordenadas possuem sinal (+, –), logo, esse ponto pertence ao 4º quadrante.
III → Falsa. O eixo horizontal é conhecido também como eixo das abcissas.
Questão 2 - No plano cartesiano a seguir, foram marcados alguns pontos:
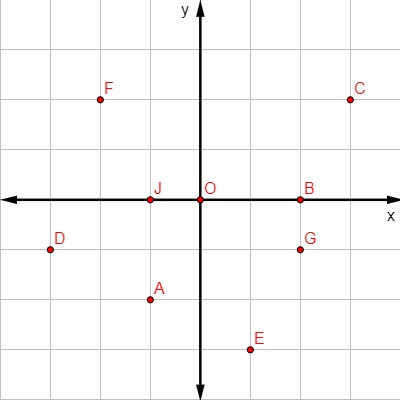
As coordenadas do ponto E e do ponto F são, respectivamente:
A) (-3, 1) e (2, -2)
B) (1, 3) e (2, 2)
C) (2, -2) e (3, -1)
D) (-2, 2) e (1, -3)
E) (2, 2) e (1, 3)
Resolução
Alternativa D
Analisando o plano cartesiano, podemos perceber que o ponto E está a 2 unidades da origem em relação ao eixo x, mas note que é para a esquerda, ou seja, x = -2.
Analisando o eixo vertical, o ponto está a 2 unidades da origem para o lado positivo do eixo y, logo, y = 2 e sua coordenada é (-2, 2).
Analisando o ponto F, ele está a 1 unidade no eixo x e a -3 unidades no eixo y, então, sua coordenada é (1, -3).
As coordenadas de E e F são, respectivamente, (-2, 2) e (1, -3).