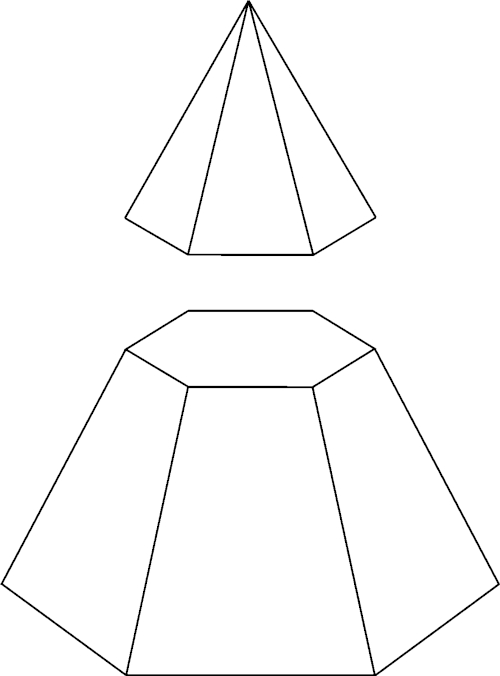
Pirâmides são poliedros que possuem uma base poligonal e, no lado oposto a essa base, um vértice. Para defini-las, podemos dizer que elas são um conjunto de segmentos de reta que ligam um polígono a um ponto fora do plano que o contém.

Elementos de uma pirâmide
-
Faces: são todos os polígonos que podem ser encontrados na superfície da pirâmide.
-
Base: nas pirâmides, a base é o polígono que aparece na definição. A base é a única face de uma pirâmide que pode ser um polígono qualquer;
-
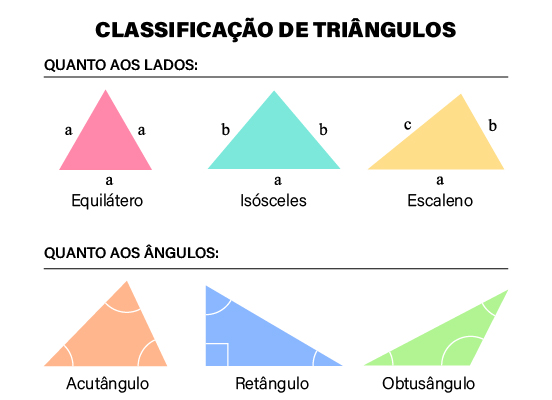
Faces laterais: todas as faces que não são a base. Toda face lateral de uma pirâmide é um triângulo;
-
Arestas: são as linhas formadas pelo encontro entre duas faces de uma pirâmide;
-
Arestas da base: são as arestas que também pertencem à base de uma pirâmide;
-
Arestas laterais: são as arestas que tocam o vértice de uma pirâmide;
-
Vértices: são os pontos de encontro de arestas de uma pirâmide;
-
Vértice da pirâmide: é o ponto de encontro de todas as arestas laterais de uma pirâmide.
.jpg)
Pirâmides regulares
Para que uma pirâmide seja regular, basta que sua base seja um polígono regular e que a projeção ortogonal de seu vértice coincida com o centro da base. Lembre-se de que um polígono regular é aquele que possui todos os lados congruentes e os ângulos internos com a mesma medida.
A partir dessa dessa definição, podemos dizer que, nas pirâmides regulares, suas faces laterais são triângulos congruentes e suas arestas laterais possuem a mesma medida.
Classificação de pirâmides
A classificação das pirâmides é feita com relação ao número de lados que possui a sua base. Assim, uma pirâmide cuja base é um triângulo é chamada de pirâmide triangular; uma pirâmide cuja base é um quadrilátero é chamada de pirâmide quadrangular; se a base for um pentágono, a pirâmide será pentagonal, e assim por diante.
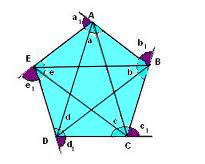
Veja um exemplo de uma pirâmide pentagonal em que a base é um polígono não convexo.

Volume da pirâmide
O volume da pirâmide é determinado pela seguinte equação:
V = Ab·h
3
-
V: volume da pirâmide;
-
Ab: a área da base;
-
h: altura.
Veja um exemplo:
Um reservatório tem formato de pirâmide de base retangular. O comprimento da base é 12 metros e seu perímetro mede 36 metros. Sabendo que a altura dessa pirâmide é de 15 metros, calcule sua capacidade.
Solução: A capacidade de um sólido geométrico é seu volume. Para calcular o volume dessa pirâmide, é necessário descobrir a área de sua base e, para isso, temos que calcular a largura dessa base.
Observe que um dos lados da base mede 12 m. O lado oposto a ele também mede 12 metros, pois lados opostos de um retângulo são congruentes. Sobram 12 metros para serem distribuídos entre os lados restantes, que também são opostos. Assim, serão 5 metros para cada. O perímetro da base dessa pirâmide, portanto, é o resultado da seguinte soma: 12 + 12 + 6 + 6 = 36. Logo, as medidas dos lados da base são 12 m e 6 m.
A área do retângulo é o produto entre sua altura e base, que também podem ser chamadas de comprimento e largura. Logo, a área da base dessa pirâmide é:
Ab = 12·6 = 72 m2
O volume, portanto, é:
V = Ab·h
3
V = 72·15
3
V = 1080
3
V = 360 m3
Assim, a capacidade do reservatório é 360 m2.
Aproveite para conferir nossa videoaula sobre o assunto: