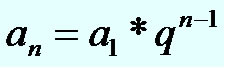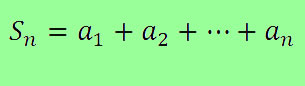Dada uma sequência numérica onde a partir do 2º termo se dividirmos qualquer número pelo seu antecessor e o resultado for um número constante recebe o nome de progressão geométrica de razão q.
Veja alguns exemplos de sequências numéricas que são progressões geométricas:
(2, 6, 18, 54, 162, 486, 1458, 4374,...) razão q = 3, pois 6:2 = 3
(-5, 15, -45, 135, -405, 1215, ...) razão q = -3, pois 135:(-45) = -3
(3, 15, 75, 375, 1875, 9375,...) razão q = 5, pois 9375:1875 = 5
Uma P.G. pode ser classificada de acordo com a sua razão (q).
Alternada ou oscilante: quando q < 0.
Crescente: quando [a1 > 0 e q > 1] ou [a1 < 0 e 0 < q < 1].
Decrescente: quando [a1 > 0 e 0 < q < 1] ou [a1 < 0 e q >1]
Termo Geral de uma P.G.
Conhecendo o primeiro termo (a1) e a razão (q) de uma progressão geométrica determinamos qualquer termo, basta utilizarmos a seguinte expressão matemática:
an = a1*qn – 1
Exemplos
a5 = a1 * q4
a12 = a1 * q11
a15 = a1 * q14
a32 = a1 * q31
a100 = a1 * q99
Exemplo 1
Determine o 9º termo da P.G. (2, 8, 32,...).
a1 = 2
q = 8:2 = 4
an = a1 * qn-1
a9 = a1 * q9-1
a9 = 2 * 48
a9 = 2 * 65536
a9 = 131072
Exemplo 2
Dada a P.G. (3, -9, 27, -81, 243, -729, ...), calcule o 14º termo.
a1 = 3
q = -9:3 = -3
an = a1 * qn-1
a14 = 3 * (-3)14-1
a14 = 3 * (-3)13
a14 = 3 *(-1.594.323)
a14 = -4.782.969
Exemplo 3
Calcule o 8º termo da P.G. (-2, -10, -50, -250, ...).
a1 = -2
q = (-10):(-2) = 5
an = a1 * qn-1
a8 = -2 * q8-1
a8 = -2 * 57
a8 = -2 * 78.125
a8 = -156.250
As progressões possuem diversas aplicações, um bom exemplo são as estações do ano que se repetem obedecendo a um determinado padrão. No Egito antigo os povos se baseavam em estudos sobre progressões no intuito de saberem os períodos de enchente do rio Nilo, para organizarem suas plantações.
Videoaulas relacionadas: