Operações com conjuntos

As operações com conjuntos são essenciais para compreender a relação entre um ou mais conjuntos numéricos. Recorrentes no estudo da álgebra, são elas:

• união, que é a junção de todos os elementos dos conjuntos;

• intersecção, que são os elementos que pertencem simultaneamente a dois conjuntos;

• diferença, que são os elementos que pertencem ao primeiro e não pertencem ao segundo conjunto;

• conjunto complementar, que é um caso particular de diferença entre dois conjuntos.

Leia também: Operações matemáticas básicas

Tópicos deste artigo

• 1 - União de conjuntos
• 2 - Intersecção de conjuntos
• 3 - Diferença
• 4 - Conjunto complementar
• 5 - Exercícios resolvidos

União de conjuntos

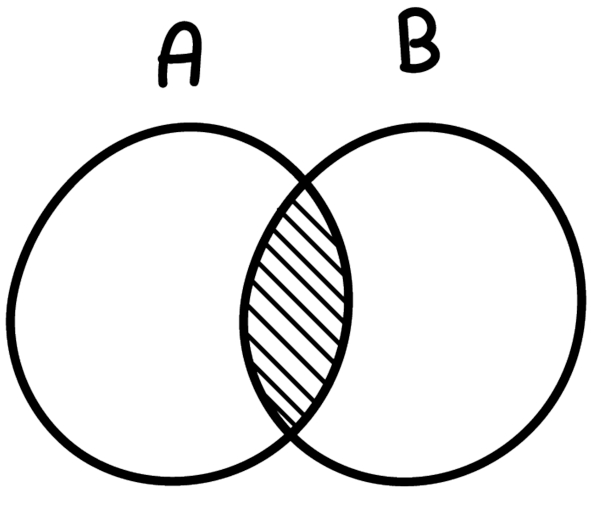
Na teoria de conjuntos, chamamos de união entre dois ou mais conjuntos o conjunto formado pela junção de todos os termos. Utilizamos para representar a união o símbolo A U B (A união com B).

No nosso dia a dia, é bastante comum a divisão de elementos em conjuntos. Por exemplo, na biologia, temos a união de vários seres vivos, que são divididos em grupos menores de acordo com as suas características. Podemos dizer também, por exemplo, que o território brasileiro é formado pela união de seus estados.

Exemplo

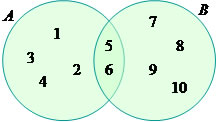
Dados os conjuntos A={1,2,3,4,5} e B={4,5,6,7,8}, a união de A com B é representada por:

A U B = {1,2,3,5,6,7,8}

É possível também realizar a representação desses conjuntos por meio do diagrama a seguir:

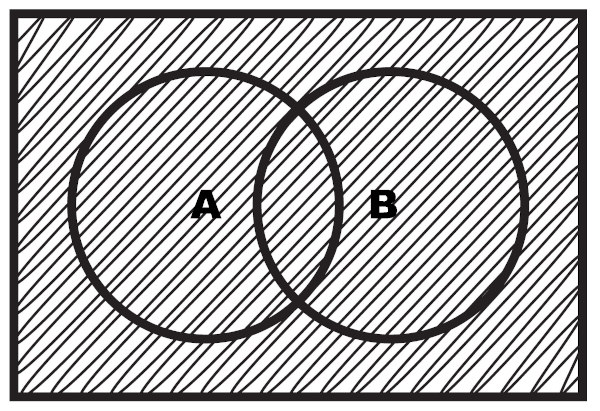
Intersecção de conjuntos

A intersecção de dois ou mais conjuntos é composta pelos elementos que pertencem simultaneamente a todos esses conjuntos. Essa operação também é bastante comum no nosso dia a dia.

Exemplo 1

Seja A={1,2,3,4,5} e B={4,5,6,7,8}, a intersecção de A com B (A∩B) é representada por:

A ∩ B= {4,5}

É possível também realizar a representação da intersecção por meio de diagrama. A intersecção é a região em destaque que fica entre os dois conjuntos.

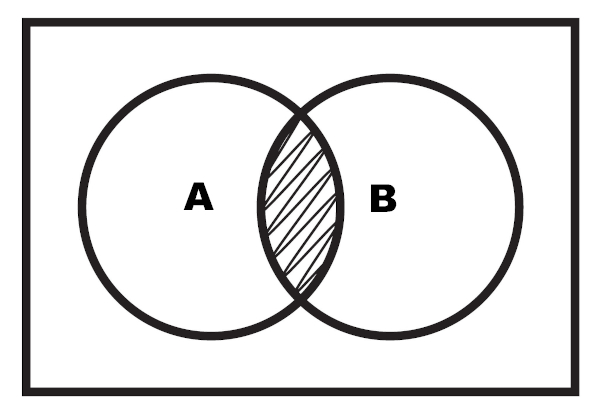
Exemplo 2

Podemos escrever os conjuntos dos rios que banham o estado de Goiás: G: {Aporé, Araguaia, Claro, Corumbá, dos Bois, Paranã, Paranaíba, Maranhão, São Marcos}. Também podemos escrever o conjunto dos rios que banham o estado de Tocantins: T: {Tocantins, Araguaia, do Sono, das Balsas, Paranã, Manuel Alves}.

A intersecção entre esses conjuntos pode ser representada por:

G∩T {Araguaia}

Diferença

Definimos como diferença entre dois conjuntos a operação A – B, que tem como resultado os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.

Exemplo

Seja A: {1,2,3,4,5} e B {4,5,6,7,8}, a diferença entro o conjunto A e o conjunto B é igual a:

A – B = {1,2,3}

Note que a ordem é importante, pois a diferença entre o conjunto B e o conjunto A é igual a:

B – A = {6,7,8}

Essa diferença pode também ser representada por meio do diagrama a seguir:

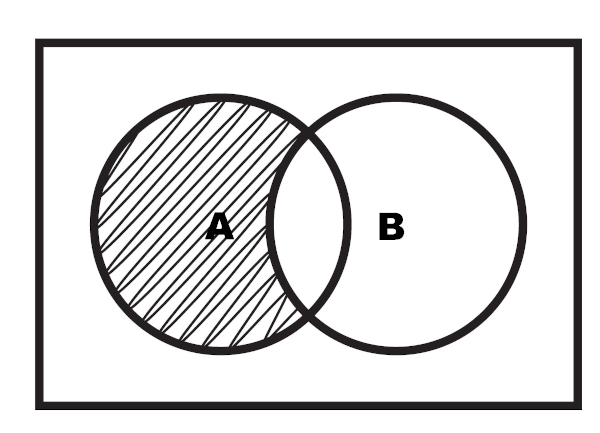
Conjunto complementar

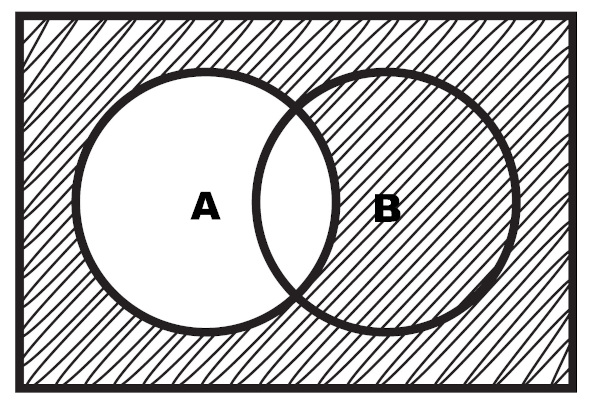
Tratado como um caso especial de diferença entre dois conjuntos, precisamos definir antes o que é o conjunto universo. Conhecemos como conjunto universo o conjunto formado por todos os elementos de um espaço amostral a ser definido, como os números de 1 até 20 ou todos os números reais, enfim, cada situação possui um conjunto universo determinado.

O conjunto complementar de A, denotado por A^c, é o conjunto formado por todos os elementos que pertencem ao universo U e não pertencem ao conjunto A, ou seja, o complementar de um conjunto quando se conhece o conjunto universo U é igual a U – A .

Exemplo

Dado o universo U de todos os números de 1 até 16, ou seja:

U = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

E seja A = {2,4,6,8,10,12,14,16} o conjunto complementar de A, ou seja:

A^c = {1,5,7,8,10,11,12,13,15}

Leia também: Quatro conteúdos básicos de Matemática para o Enem

Exercícios resolvidos

1) Sabendo que A = { 1,3,5,9,11,12}, B = {0,2,5, 10, 12, 20} e C = {3,4,8,9,12,15,20}, o conjunto formado por A ∩C U B é:

a) {0,2,3,5,9,10,12,20}.

b) {3,9,12}.

c) {3,4,8,9,15,20}.

d) {0,2,3,5,9,10,20}.

Resolução:

Vamos calcular as operações separadamente.

A ∩C = { 3,12}

Então a união de A ∩C com B formará o conjunto:

A ∩CUB = {0,2,3,5,9,10,12,20}

Resposta: alternativa A.

2) Dado o conjunto dos números naturais como universo e seja P o conjunto dos números pares e A o conjunto dos números múltiplos de 3, podemos afirmar que:

I – o conjunto P^c é o conjunto dos números ímpares;

II – a intersecção de P com A é o conjunto dos números múltiplos de 6;

III – o conjunto A é formado somente por números ímpares.

Analisando as afirmativas, marque a alternativa correta.

a) Somente I é verdadeira.

b) Somente II é verdadeira.

c) Somente III é verdadeira.

d) Somente I e II são verdadeiras.

e) Somente II e III são verdadeiras.

Resolução:

I – Verdadeira.

Note que, no conjunto dos números naturais, um número pode ser par ou ímpar se queremos P^c.

P^c= N* - P, ou seja, os naturais sem os pares, logo o complementar dos números pares será os números ímpares.

II – Verdadeira.

A intersecção entre os números pares e os números múltiplos de 3 são os múltiplos de 6. Lembre-se do critério de divisibilidade por 6, que são os números divisíveis por 2 e por 3 ao mesmo tempo.

III – Falsa.

Existem múltiplos de 3 que são ímpares, como o 6, 12,18, entre outros.

Resposta: alternativa D.