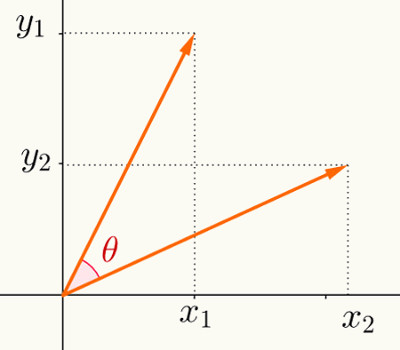Vetores são objetos matemáticos amplamente utilizados nos estudos de Mecânica, na disciplina de Física, pois eles descrevem a trajetória em linha reta de um ponto, indicando sua direção, sentido e intensidade de movimento. Esses objetos são representados geometricamente por flechas, e sua localização no espaço é dada por meio de pontos com coordenadas reais. Desse modo, é possível definir algumas das operações básicas matemáticas para os vetores.

Representação geométrica do vetor v = (x,y), que possui início na origem e fim no ponto A = (x,y)
O ponto A = (x,y) pertencente ao plano pode ser usado para definir um vetor v = (x,y). Para isso, esse vetor deve ter seu início na origem O = (0,0) e seu fim no ponto (x,y), com as componentes x e y pertencentes ao conjunto dos números reais.
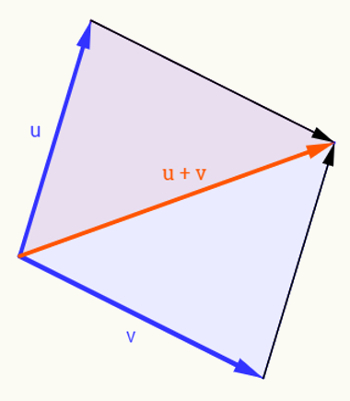
Adição de vetores
Dados os vetores u = (a,b) e v = (c,d), a operação adição deve ser definida da seguinte maneira: As coordenadas do vetor resultante, u + v, serão a soma das respectivas coordenadas dos vetores u e v:
u + v = (a + c, b + d)
Como as coordenadas resultantes são obtidas por meio de somas de números reais, é possível mostrar que a soma de vetores é comutativa e associativa, além da existência de elemento neutro e elemento inverso aditivo. Essas propriedades são, respectivamente:
i) u + v = v + u
ii) (u + v) + w = u + (v + w), sendo w um vetor pertencente ao mesmo plano que u e v.
iii) v + 0 = 0 + v = v
iv) v – v = – v + v = 0
Subtração de vetores
A subtração do vetor u = (a,b) pelo vetor v = (c,d) é definida como a soma entre o vetor u e o vetor – v = (– c, – d). Desse modo, teremos:
u – v = u + (– v) = (a – c, b – d)
Multiplicação de vetor por um número real
Seja u = (a,b) um vetor e k um número real, a multiplicação do vetor u pelo número real k é dada por:
k·u = k·(a,b) = (k·a,k·b)
Considerando que k, i, a e b são números reais, para vetores multiplicados por um número real, valem as seguintes propriedades: comutatividade, associatividade, distributividade e existência de elemento neutro. Respectivamente, essas propriedades são traduzidas como:
i) k·u = u·k
ii) k·(i·v) = k·i·(v)
iii) k·(u + v) = k·u + k·v
iv) 1·v = v·1 = v
Módulo de um vetor
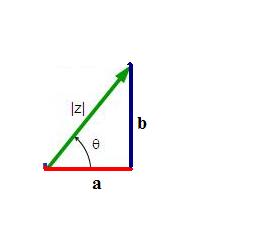
Vetores são representados geometricamente como segmentos de reta orientados para que sejam capazes de indicar sentido e direção. Dessa forma, como segmento de reta, qualquer vetor pode ter seu comprimento medido. Essa medida de comprimento também recebe o nome de módulo de um vetor por indicar a distância entre o ponto final desse vetor e a origem (assim como módulo de um número real). Outra denominação frequente dessa medida é norma de um vetor.
A norma ou módulo do vetor v = (a,b) é denotada por |v| e pode ser calculada por meio da distância entre o ponto (a,b) e o ponto (0,0), já que esses são o ponto final e o inicial do vetor v, respectivamente. Dessa forma, escrevemos:

Cálculos feitos para encontrar a norma de v
Produto interno
Sejam os vetores u = (a,b) e v = (c,d), o produto interno entre eles, denotado por ![]() , é definido pela seguinte expressão:
, é definido pela seguinte expressão:
![]()
δ é o ângulo entre os vetores u e v. Outra maneira de calcular o produto interno entre dois vetores é a seguinte:
![]()
Aproveite para conferir nossa videoaula relacionada ao assunto: