Os números surgiram na sociedade para atender à necessidade do ser humano de realizar a contagem de quantidades, bem como de representar ordem e medidas. Com o passar do tempo e com o desenvolvimento das civilizações, foi preciso criar os números.
Os conjuntos numéricos surgiram no decorrer desse desenvolvimento. Os principais conjuntos numéricos estudados são os que abarcam números naturais, números inteiros, números racionais, números irracionais e números reais. Existe outro conjunto numérico, menos usual, que é o conjunto dos números complexos.
O sistema indo-arábico é o sistema que utilizamos para representar os números. Ele conta com os algarismos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Existem outros sistemas de numeração, como o romano.
Leia também: Sistema de numeração decimal — aquele que utilizamos para representar quantidades
Tópicos deste artigo
- 1 - Resumo sobre os números
- 2 - O que são números?
- 3 - História dos números
- 4 - Conjuntos numéricos
- 5 - Outros números
- 6 - Exercícios resolvidos sobre números
Resumo sobre os números
-
Os números são símbolos utilizados para representar quantidade, ordem ou medida.
-
Os conjuntos numéricos surgiram ao longo do tempo, de acordo com as necessidades humanas, sendo eles:
O que são números?
Os números são símbolos utilizados para representar quantidades, ordem ou medidas. Eles são objetos primitivos da Matemática e foram desenvolvidos aos poucos, junto da escrita.
Atualmente, para representar os números, utilizamos o sistema decimal indo-arábico, que utiliza os algarismos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Os números que representam quantidades (1, 2, 3, 4 ...) são conhecidos como cardinais. Já os números que representam ordem (1º, 2º, 3º ... — primeiro, segundo, terceiro etc.) são conhecidos como números ordinais.
História dos números
A história dos números acompanhou a história da evolução do ser humano. Precisando contabilizar, o ser humano utilizou o instrumento mais próximo a ele, o próprio corpo (os dedos das mãos), para representar quantidades do dia a dia. Por causa da necessidade de registro, houve o desenvolvimento da escrita e, consequentemente, da representação dos números.
Ao longo da história da humanidade, foram desenvolvidas várias formas de escrita, com lógicas próprias, pelos mais diversos povos, como os sumérios, os egípcios, os maias, os chineses, os romanos etc. Cada sistema de numeração atendia às necessidades da época, se adaptando quando necessário.
Hoje, para a realização de cálculos, o sistema de numeração utilizado é o indo-arábico. Nesse sistema, há uma base 10, sendo ele posicional. O sistema indo-arábico é o mais conveniente na atualidade pela facilidade na realização de operações matemáticas e pela possibilidade de representação de qualquer medida, ordem ou quantidade com apenas 10 símbolos, os algarismos.
Leia também: Três curiosidades sobre os números
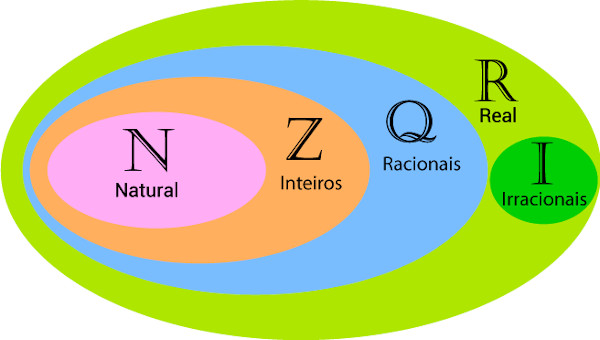
Conjuntos numéricos
Os conjuntos numéricos surgiram no decorrer do tempo, com início no conjunto dos números naturais e desenvolvimento nos conjuntos dos números inteiros, racionais e reais. Vejamos, a seguir, cada um deles.
-
Conjunto dos números naturais
Os números naturais são os mais simples que conhecemos. O conjunto dos números naturais é representado por e é formado pelos números mais comuns no nosso dia a dia, utilizados para quantificar. São eles:
\(\mathbb{N}\) = {0, 1, 2, 3, 4, 5, ...}
-
Conjunto dos números inteiros
Com o surgimento das relações comerciais, tornou-se necessária a ampliação do conjunto dos números naturais, pois precisava-se também representar números negativos. O conjunto dos números inteiros é representado pela letra e é composto pelos números:
\(\mathbb{Z}\ \) = {... – 3, – 2, –1, 0, 1, 2, 3 ...}
-
Conjunto dos números racionais
O conjunto dos números racionais surgiu da necessidade do ser humano em medir. Durante o estudo de medidas, foi preciso representar números decimais e frações. Assim, o conjunto dos números racionais é composto por todos os números que podem ser representados como fração. Sua notação é a seguinte:
\(\mathbb{Q}={x\ \epsilon\ \mathbb{Q}\rightarrow x=\frac{a}{b},a\ e\ b\ \epsilon\ \mathbb{Z},b\neq0}\)
-
Conjunto dos números irracionais
O conjunto dos números irracionais foi descoberto durante a resolução de problemas envolvendo o teorema de Pitágoras. Ao se deparar com números como a , o ser humano percebeu que nem todos os números podem ser representados como fração. As dízimas não periódicas e as raízes não exatas fazem parte desse conjunto.
-
Conjunto dos números reais
Para unir os conjuntos dos números racionais e dos números irracionais criou-se o conjunto dos números reais. Ele é o conjunto mais comum para problemas envolvendo relações entre conjuntos, como no estudo das funções.
➝ Videoaula sobre conjuntos numéricos
Outros números
O conjunto dos números complexos é representado pela letra e é uma ampliação do conjunto dos números reais. Nele estão inclusas as raízes de números negativos. No estudo dos números complexos, a é representada por i. Os números complexos possuem várias aplicações quando a Matemática é estudada de forma mais aprofundada.
Leia também: Operações matemáticas básicas — os primeiros passos das relações numéricas
Exercícios resolvidos sobre números
Questão 1
Sobre os conjuntos numéricos, julgue as afirmativas a seguir:
I – Todo número negativo é considerado um número inteiro.
II – As frações não são números inteiros.
III – Todo número natural é também um número inteiro.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Resolução:
Alternativa A
I – Falsa
Os números que são escritos como fração e são negativos não são inteiros, mas sim racionais.
II – Verdadeira
As frações são números racionais.
III – Verdadeira
O conjunto dos números inteiros é uma ampliação do conjunto dos números naturais, o que faz com que todo número natural seja inteiro.
Questão 2
Analise os números a seguir:
I) \(\ \frac{1}{2} \)
II) \(-0,5\ \)
III) \(\sqrt3\)
IV) \(-\ 4\ \)
Marque a alternativa correta.
A) Todos esses números são racionais.
B) Os números II e IV são inteiros.
C) O número III não é um número real.
D) Os números I, II e IV são racionais.
E) O número III é um número racional.
Resolução:
Alternativa D
Apenas o número III não é um número racional, logo os números I, II e IV são números racionais.