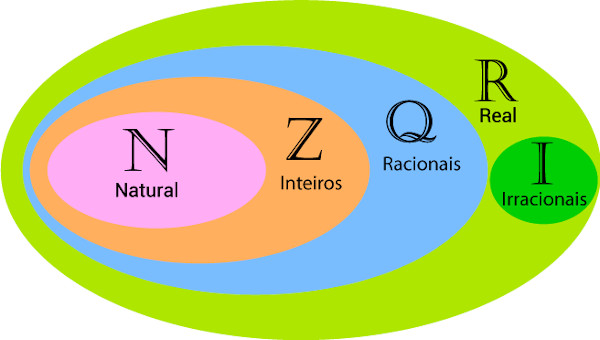
Os números reais são os elementos do conjunto R, formado pela união entre os conjuntos dos racionais (Q) e dos irracionais (I). Isso significa que o conjunto dos números reais engloba a maior parte dos números utilizados no cotidiano.
São exemplos de números reais os números inteiros, os números fracionários e as raízes não exatas.
Leia também: Quais são os conjuntos numéricos?
Tópicos deste artigo
- 1 - Resumo sobre números reais
- 2 - Quais são os números reais?
- 3 - Conjunto dos números reais
- 4 - Subconjunto dos números reais
- 5 - Representação dos números reais na reta numéricas
- 6 - Operações com números reais
- 7 - Quais são as propriedades dos números reais?
- 8 - Exercícios resolvidos sobre números reais
Resumo sobre números reais
- A união entre o conjunto dos números racionais e o conjunto dos números irracionais forma o conjunto dos números reais.
- O conjunto dos números reais é representado pela letra R.
- São subconjuntos de R os conjuntos dos números naturais (N), inteiros (Z), racionais (Q) e irracionais (I).
- Cada ponto na reta numérica indica a posição de um número real.
Quais são os números reais?
Todos os números racionais e irracionais são números reais. Assim, é fundamental conhecer os conjuntos (Q) e (I) para compreender os números reais.
Exemplos:
- 3 é real, pois 3 é racional.
- -10 é real, pois -10 é racional.
- \(\sqrt5\) é real, pois \(\sqrt5\) é irracional.
- π é real, pois π é irracional.
Conjunto dos números reais
O conjunto dos números reais é representado pela letra R e corresponde à união entre o conjunto dos números racionais (Q) e o conjunto dos números irracionais (I).
\(R=Q\cup I\)
Portanto, como observamos nos exemplos, se um elemento pertence ao conjunto dos números reais, então deve pertencer ao conjunto dos números racionais ou ao conjunto dos números irracionais.
Subconjunto dos números reais
Observe que o conjunto dos números racionais (Q) possui dois subconjuntos importantes: o conjunto dos números naturais (N) e o conjunto dos números inteiros (Z). Como R= Q∪I , então (N) e (Z) também são subconjuntos de R.
Assim, os principais subconjuntos de R são:
- (N) – conjunto dos números naturais;
- (Z) – conjunto dos números inteiros;
- (Q) – conjunto dos números racionais;
- (I) – conjunto dos números irracionais.
Outros subconjuntos de R:
- R* – conjunto dos números reais não nulos;
- R+ – conjunto dos números reais positivos;
- R- – conjunto dos números reais negativos.
Representação dos números reais na reta numéricas
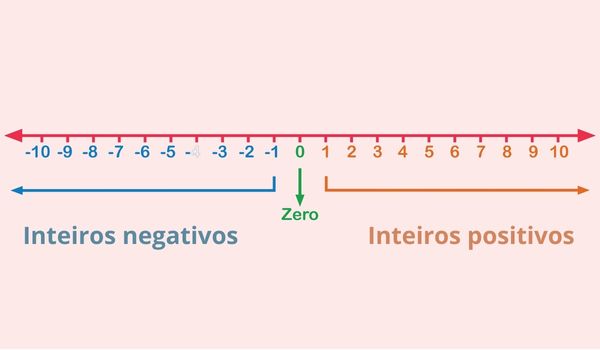
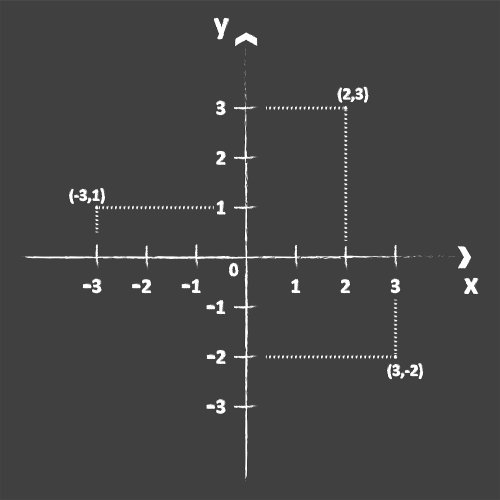
A reta numérica, também conhecida como reta real, expressa a posição de todos os números reais em relação ao zero, chamado de origem. À esquerda do zero, apresentam-se os números negativos, e, à direita, os números positivos, distribuídos em ordem crescente da esquerda para a direita.

Operações com números reais
As operações com números reais seguem as mesmas estruturas que as operações com números dos outros conjuntos numéricos mencionados. Vejamos um exemplo para cada operação.
- Adição: \(60+4=64\)
- Subtração: \(22-3=19\)
- Multiplicação: \(1,5\cdot7=10,5\)
- Divisão: \(-\frac{5}{11}\div\frac{1}{8}=-\frac{40}{11}\)
- Potenciação: \(6^5=7776\)
- Radiciação: \(\sqrt{225}=15\)
Quais são as propriedades dos números reais?
-
Comutatividade
A propriedade comutativa é válida para as operações de adição e multiplicação. Se a e b são números reais, então:
\(a+b=b+a\ \)
\(a\cdot b=b\cdot a\)
Exemplos:
\(2+3=5 e 3+2=5\)
\(\frac{1}{3}\cdot\frac{1}{2}=\frac{1}{6} e \frac{1}{2}\cdot\frac{1}{3}=\frac{1}{6}\)
-
Associatividade
A propriedade associativa é válida para as operações de adição e multiplicação. Se a , b e c são números reais, então:
\(a+\left(b+c\right)=\left(a+b\right)+c\)
\(a\cdot\left(b\cdot c\right)=\left(a\cdot b\right)\cdot c\)
Exemplos:
\(0,2+\left(1,4+0,8\right)=2,4 e \left(0,2+1,4\right)+0,8=2,4\)
\(-3\cdot\left(7\cdot1\right)=-21 e \left(-3\cdot7\right)\cdot1=-21\)
-
Elemento neutro
A propriedade do elemento neutro é válida para as operações de adição e multiplicação. Se a é um número real, então:
\(a+0=a\)
\(a\cdot1=a\)
Exemplos:
\(5+0=5\)
\(\ 8\cdot1=8\)
-
Elemento oposto
A propriedade do elemento oposto é válida para as operações de adição e multiplicação. Se a é um número real, então:
\(a+\left(-a\right)=0\)
\(a\cdot\frac{1}{a}=1\)
Exemplos:
\(0,8+\left(-0,8\right)=0\)
\(20\cdot\frac{1}{20}=1\)
-
Distributiva
Se a e b são números reais, então:
\(a\cdot\left(b+c\right)=a\cdot b+a\cdot c\)
Exemplo:
\(\sqrt2\cdot\left(3+7\right)=10\sqrt2 e \sqrt2\cdot3+\sqrt2\cdot7=10\sqrt2\)
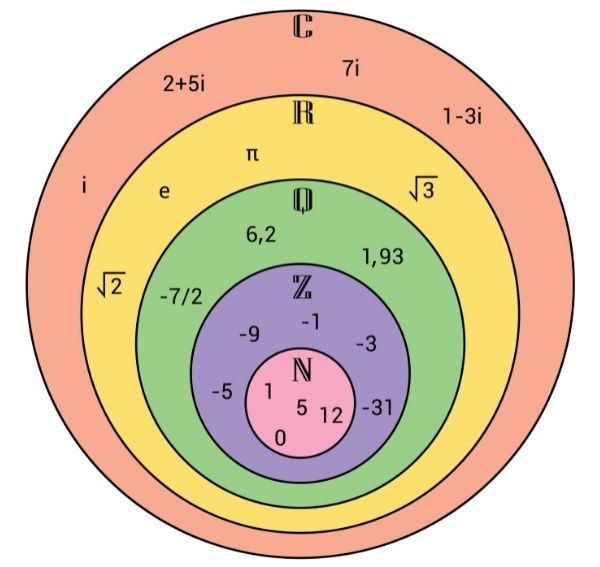
Leia também: Números complexos — conjunto que surgiu para ampliar os números reais
Exercícios resolvidos sobre números reais
Questão 1
Classifique cada afirmação abaixo em V (verdadeira) ou F (falsa).
I. R⊂Q
II. O número π é real.
III. Z⊂R
A ordem correta, de cima para baixo, é:
a) V-V-F
b) F-V-V
c) V-F-V
d) F-F-F
e) V-F-F
Resolução: alternativa B
A afirmação I é falsa, pois R não é subconjunto de Q. O número \(\sqrt3\), por exemplo, é um número real, mas não é racional.
A afirmação II é verdadeira. π é um número irracional e, portanto, é um número real.
A afirmação III é verdadeira, pois Z é um subconjunto de R.
Questão 2
Considere as afirmações abaixo.
I. \( –2,1759∈R\)
II. As dízimas periódicas são números reais.
III. Todos os números reais são racionais ou irracionais.
Está correto o que se afirma em:
a) I, apenas.
b) II, apenas.
c) III, apenas.
d) I e II, apenas.
e) I, II e III.
Resolução: alternativa E
A afirmação I está correta, pois -2,1759 pertence ao conjunto dos números reais, uma vez que é um número racional.
A afirmação II está correta, pois as dízimas periódicas são números racionais e, portanto, são números reais.
A afirmação III está correta, pois \(R=Q\cup I\).